开源有限元软件FEniCS小记

FEniCS
组成部分
- FEniCSx
- FEniCS
安装
如何使用？
参考

FEniCS

作为一项科研合作，FEniCS 项目2003年由芝加哥大学（University of Chicago）和查尔姆斯理工大学（Chalmers University of Technology）发起。

注意，FEniCS 采用比较宽松的 LGPL 协议发布！！！

2019年重构后的新版本叫做FEniCSx，其重要组成部分是DOLFINx，可以在C++或Python下使用。

fenics

组成部分

似乎很乱：

初始版本FEniCS：包括 DOLFIN、FIAT
后来FEniCS扩展成：DOLFIN、FFC、FIAT、UFL
再后来（2019）FEniCSx：重构为 DOLFINx、FFCx、Basix、UFL

FEniCSx

Basix：一个用于生成有限元基函数（finite element basis functions）的库，支持任意阶的有限元计算。它是 FEniCSx 中的核心组件之一，负责提供灵活且高效的有限元基础功能。
UFL（统一形式语言，Unified Form Language）：一个嵌入在 Python 中的领域特定语言（domain-specific language），用于定义有限元变分形式（finite element variational forms）。UFL 是 FEniCSx 中描述微分方程离散化的核心语言。
FFCx（FEniCSx 形式编译器，FEniCSx Form Compiler）：一个专门用于将 UFL 定义的变分形式编译成高效低级代码的工具。FFCx 是 FEniCSx 的编译引擎，生成与 Basix 和 DOLFINx 兼容的代码。
DOLFINx：FEniCSx 的高性能计算核心库，基于 C++ 和 Python。它提供数据结构和算法支持，包括有限元网格（finite element meshes）、装配（assembly）、求解器（solvers），以及与线性代数工具的接口。DOLFINx 是 FEniCSx 的用户接口和计算核心。

在IO上，它涉及到

Gmsh
VTK
PyVista
ADIOS2

线性代数后端上，它涉及到

NumPy
PETSc
Trilinos
Eigen

FEniCS

先看看老的FEnics

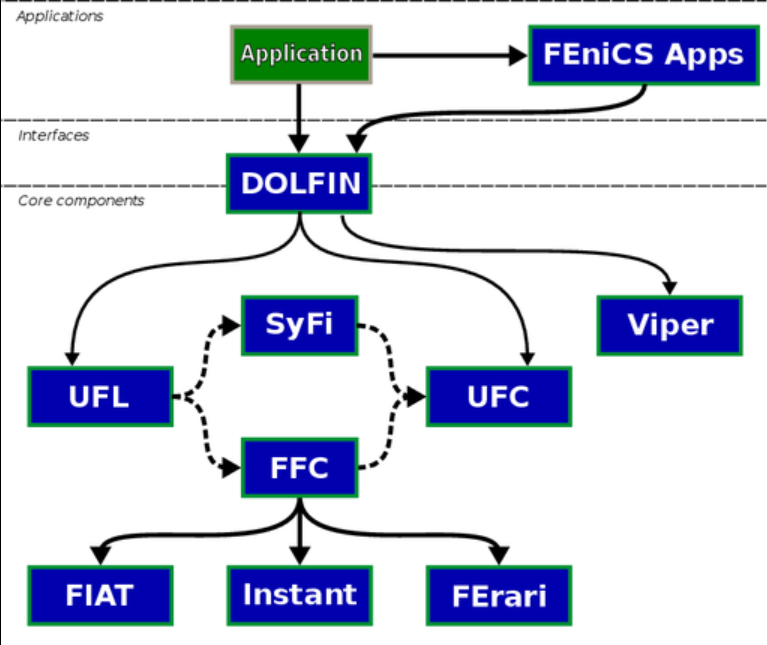
fenics

UFL（统一形式语言，unified form language）：一种嵌入在 Python 中的领域特定语言，用于通过有限元变分形式（finite element variational forms）描述微分方程的有限元离散化。
FIAT（有限元自动生成器，finite element automatic tabulator）：FEniCS 的有限元后端，是一个 Python 模块，用于生成单纯形（simplices）上的任意阶有限元基函数（finite element basis functions）。
FFC（FEniCS 形式编译器，FEniCS form compiler）：一个编译器，用于将 UFL 代码作为输入并生成 UFC 输出。
UFC（统一形式装配代码，unified form-assembly code）：一个 C++ 接口，由用于评估和装配有限元变分形式的低级函数组成。
Instant：一个 Python 模块，用于在 Python 中内联 C 和 C++ 代码。
DOLFIN：一个 C++/Python 库，提供有限元网格（finite element meshes）、自动化有限元装配（automated finite element assembly）以及数值线性代数（numerical linear algebra）的数据结构和算法。

安装

在Ubuntu或Windows的WSL2下：

sudo add-apt-repository ppa:fenics-packages/fenics
sudo apt update
sudo apt install fenicsx

另外，它还支持 conda 和 docker 方式

如何使用？

基本步骤

创建网格和定义有限元空间；
设置边界条件并定义变分问题；
求解线性方程并输出结果；
使用 pyvista 可视化计算结果。

具体怎么做？？找个具体例子

泊松方程求解问题

\Gamma_{D}：Dirichlet 边界条件规定了解 u 在边界上的值。例如，温度的值或位势的值。 \Gamma_{N}：Neumann 边界条件规定了解的法向导数（即变化率），而不是解本身的值。

对于一个区域 \Omega \subset \mathbb{R}^n ，其边界为 \partial \Omega = \Gamma_{D} \cup \Gamma_{N}，泊松方程在特定边界条件下的形式为：

\begin{align} \nabla^{2} u &= f \quad {\rm in} \ \Omega, \\ u &= 0 \quad {\rm on} \ \Gamma_{D}, \\ \nabla u \cdot n &= g \quad {\rm on} \ \Gamma_{N}. \end{align}

其中，f 和 g 是已知的输入数据，n 表示指向外部的边界法线。变分问题可以表述为：寻找 u \in V，使得

a(u, v) = L(v) \quad \forall \ v \in V,

其中 V 是一个适当的函数空间，且

\begin{align} a(u, v) &:= \int_{\Omega} \nabla u \cdot \nabla v \, {\rm d} x, \\ L(v) &:= \int_{\Omega} f v \, {\rm d} x + \int_{\Gamma_{N}} g v \, {\rm d} s. \end{align}

其中，a(u, v) 是双线性形式，L(v) 是线性形式。假设函数空间 V 中的所有函数都满足 Dirichlet 边界条件（即 u = 0 \ {\rm on} \ \Gamma_{D}）。

具体例子

考虑以下内容：

\Omega = [0,2] \times [0,1]（矩形区域）
\Gamma_{D} = \{(0, y) \cup (2, y) \subset \partial \Omega\}（Dirichlet 边界）
\Gamma_{N} = \{(x, 0) \cup (x, 1) \subset \partial \Omega\}（Neumann 边界）
g = \sin(5x)（Neumann 边界条件）
f = 10\exp(-((x - 0.5)^2 + (y - 0.5)^2) / 0.02)（源项）

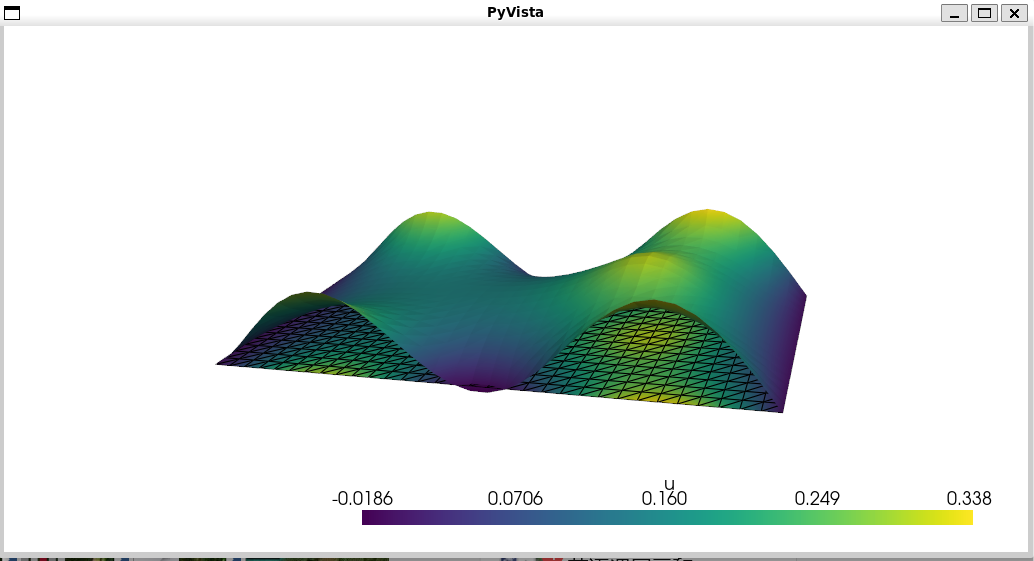
最终结果：

fenics

对应代码：

import ufl
import dolfinx
import mpi4py
import numpy as np
from petsc4py.PETSc import ScalarType
from dolfinx.fem.petsc import LinearProblem

msh = dolfinx.mesh.create_rectangle(
    comm=mpi4py.MPI.COMM_WORLD,
    points=((0.0, 0.0), (2.0, 1.0)),
    n=(32, 16),
    cell_type=dolfinx.mesh.CellType.triangle,
)
V = dolfinx.fem.functionspace(msh, ("Lagrange", 1))

facets = dolfinx.mesh.locate_entities_boundary(
    msh,
    dim=(msh.topology.dim - 1),
    marker=lambda x: np.isclose(x[0], 0.0) | np.isclose(x[0], 2.0),
)

dofs = dolfinx.fem.locate_dofs_topological(V=V, entity_dim=1, entities=facets)

bc = dolfinx.fem.dirichletbc(value=ScalarType(0), dofs=dofs, V=V)

u = ufl.TrialFunction(V)
v = ufl.TestFunction(V)
x = ufl.SpatialCoordinate(msh)
f = 10 * ufl.exp(-((x[0] - 0.5) ** 2 + (x[1] - 0.5) ** 2) / 0.02)
g = ufl.sin(5 * x[0])
a = ufl.inner(ufl.grad(u), ufl.grad(v)) * ufl.dx
L = ufl.inner(f, v) * ufl.dx + ufl.inner(g, v) * ufl.ds

problem = LinearProblem(a, L, bcs=[bc], petsc_options={"ksp_type": "preonly", "pc_type": "lu"})
uh = problem.solve()

with dolfinx.io.XDMFFile(msh.comm, "out_poisson/poisson.xdmf", "w") as file:
    file.write_mesh(msh)
    file.write_function(uh)

#--------------
import pyvista

cells, types, x = dolfinx.plot.vtk_mesh(V)
grid = pyvista.UnstructuredGrid(cells, types, x)
grid.point_data["u"] = uh.x.array.real
grid.set_active_scalars("u")
plotter = pyvista.Plotter()
plotter.add_mesh(grid, show_edges=True)
warped = grid.warp_by_scalar()
plotter.add_mesh(warped)
plotter.show()

分段看看代码

创建网格和定义有限元空间

函数 create_rectangle() 用于创建一个矩形网格，定义网格的坐标范围为 (0, 0) 到 (2, 1)，并且将其分为 32x16 格，单元类型为三角形。

msh = dolfinx.mesh.create_rectangle(
    comm=mpi4py.MPI.COMM_WORLD,
    points=((0.0, 0.0), (2.0, 1.0)),
    n=(32, 16),
    cell_type=dolfinx.mesh.CellType.triangle,
)

函数 functionspace() 用于创建一个Lagrange一阶有限元空间 V，用于表示离散化后的未知函数。

V = dolfinx.fem.functionspace(msh, ("Lagrange", 1))

设置边界条件

函数 locate_entities_boundary()用于查找网格的边界，定位在 x=0 或 x=2 处的边界，用于设置边界条件。

facets = dolfinx.mesh.locate_entities_boundary(
    msh,
    dim=(msh.topology.dim - 1),
    marker=lambda x: np.isclose(x[0], 0.0) | np.isclose(x[0], 2.0),
)

函数 locate_dofs_topological() 根据边界上的元素位置，定位边界上的自由度（DOFs），这些自由度将用于施加边界条件。

dofs = dolfinx.fem.locate_dofs_topological(V=V, entity_dim=1, entities=facets)

函数 dirichletbc()设置Dirichlet边界条件，将边界自由度 dofs 上的解值设为0。

bc = dolfinx.fem.dirichletbc(value=ScalarType(0), dofs=dofs, V=V)

定义变分问题

u：试函数？表示问题中的未知数，通过TrialFunction()定义。
v：测试函数，用于在变分问题中进行积分。通过TestFunction()定义测试函数。
x：网格的空间坐标，通过SpatialCoordinate()获取。
f：定义源项 f，这是一个高斯型函数，表示问题的右侧项。
g：定义边界上的源项 g，这是一个关于 x[0] 的正弦函数。
a：变分问题的左侧，表示梯度的内积，ufl.inner(ufl.grad(u), ufl.grad(v)) 是对解的梯度和测试函数的梯度内积，ufl.dx 表示在网格区域上进行积分。
L：变分问题的右侧，包括源项 f 和边界项 g。

u = ufl.TrialFunction(V)
v = ufl.TestFunction(V)
x = ufl.SpatialCoordinate(msh)
f = 10 * ufl.exp(-((x[0] - 0.5) ** 2 + (x[1] - 0.5) ** 2) / 0.02)
g = ufl.sin(5 * x[0])
a = ufl.inner(ufl.grad(u), ufl.grad(v)) * ufl.dx
L = ufl.inner(f, v) * ufl.dx + ufl.inner(g, v) * ufl.ds

求解线性问题

LinearProblem()定义线性问题，其中
- a 和 L 分别是变分问题的左侧和右侧，
- bcs 是边界条件，
- petsc_options 配置了 PETSc 求解器的参数。
  - ksp_type 设置为 preonly，表示使用预处理器类型；
  - pc_type 设置为 lu，表示使用直接求解器。
solve()求解线性问题，得到解 uh。

problem = LinearProblem(a, L, bcs=[bc], petsc_options={"ksp_type": "preonly", "pc_type": "lu"})
uh = problem.solve()

函数XDMFFile()将解 uh 和网格 msh 输出到 XDMF 文件格式，便于后续可视化和分析。

with dolfinx.io.XDMFFile(msh.comm, "out_poisson/poisson.xdmf", "w") as file:
    file.write_mesh(msh)
    file.write_function(uh)

显示

vtk_mesh: 将 dolfinx 的有限元空间转换为 pyvista 可用的网格格式。
pyvista.UnstructuredGrid: 创建一个无结构的网格对象，用于可视化。
grid.point_data["u"]: 将解 uh 的实部赋值给网格的点数据，表示解的数值。

cells, types, x = dolfinx.plot.vtk_mesh(V)
grid = pyvista.UnstructuredGrid(cells, types, x)
grid.point_data["u"] = uh.x.array.real
grid.set_active_scalars("u")

参考

https://github.com/FEniCS
https://github.com/firedrakeproject/fiat
https://fenicsproject.org/
https://jsdokken.com/dolfinx-tutorial/
https://en.wikipedia.org/wiki/FEniCS_Project
https://docs.fenicsproject.org/dolfinx/v0.9.0/python/demos/demo_poisson.html

1+1=10

记记笔记，放松一下...

开源有限元软件FEniCS小记

FEniCS

组成部分

FEniCSx

FEniCS

安装

如何使用？

基本步骤

泊松方程求解问题

具体例子

分段看看代码

创建网格和定义有限元空间

设置边界条件

定义变分问题

求解线性问题

显示

参考