1+1=10

记记笔记，放松一下...

Mesh网格生成小记

网格（Mesh）用于计算机屏幕渲染和物理模拟，如有限元分析（Finite Element Analysis, FEA）和计算流体力学（Computational Fluid Dynamics, CFD）。通过将复杂形状（如桥梁）分解为简单单元（如三角形），我们可以对每个单元进行计算并模拟其相互作用，从而实现模拟和可视化。

网格生成（Mesh Generation）是指将连续的几何空间划分为离散的几何单元和拓扑单元的过程。

这一过程通常通过计算机算法完成，必要时可结合人工干预。网格生成的目标是创建一个既能准确反映输入域几何特征，又具有高质量（形状良好）单元的网格。同时，需要避免生成过多的单元，以免增加后续计算的难度。在对后续计算至关重要的区域，网格应更为精细（单元尺寸较小），以提高计算精度。

术语

网格生成

  • Mesh generation / Meshing（网格生成/网格划分）：指生成网格的过程。
  • Grid generation / Gridding（网格生成/网格布置）：范围更广？？包含网格优化，即通过调整网格以提高数值计算的速度或精度。
  • Tessellation（镶嵌/铺砖）：在计算机图形学和数学中，有时用作网格的同义词。

网格单元命名

  • Nodes / Points（节点）：表示0维单元，在计算几何中通常称为Vertices（顶点）。
  • Edges（边）：表示1维单元。
  • Faces / Cells / Entities（面/单元/实体）：2维或更高维的单元，具体名称视应用而定。
  • Elements（单元）：在有限元中，表示最高维的网格单元。 例如，3D网格中最高维单元是Elements，其2D子单元称为Faces。

常见单元

  • Triangles (Tris)（三角形）：二维三角形单元。简单，灵活
  • Quadrilaterals (Quads)（四边形）：二维四边形区域。对于规则几何区域比较高校，精度优于三角形网格
  • Tetrahedra (Tets)（四面体）：三维四面体单元。易于生成
  • Hexahedra (Hexes)（六面体/拓扑立方体）：六面体单元。较难生成，具有良好的数值性能。

网格类型

按几何结构分类

  • 二维网格（2D Mesh）：主要用于二维问题，常见网格类型有三角形（Triangles）和四边形（Quadrilaterals）。
  • 三维网格（3D Mesh）：主要用于三维问题，常见网格类型有四面体（Tetrahedra）、六面体（Hexahedra）、棱柱体（Prisms）和金字塔（Pyramids）。

按网格结构分类

  • 结构化网格（Structured Mesh）：网格单元按规则排列，适用于规则几何体，计算效率高。
  • 非结构化网格（Unstructured Mesh）：网格单元没有固定连接规则，适用于复杂几何形状，灵活性高。
  • 混合网格（Hybrid Mesh）：结合结构化和非结构化网格的优点，适用于规则和复杂区域。

mesh

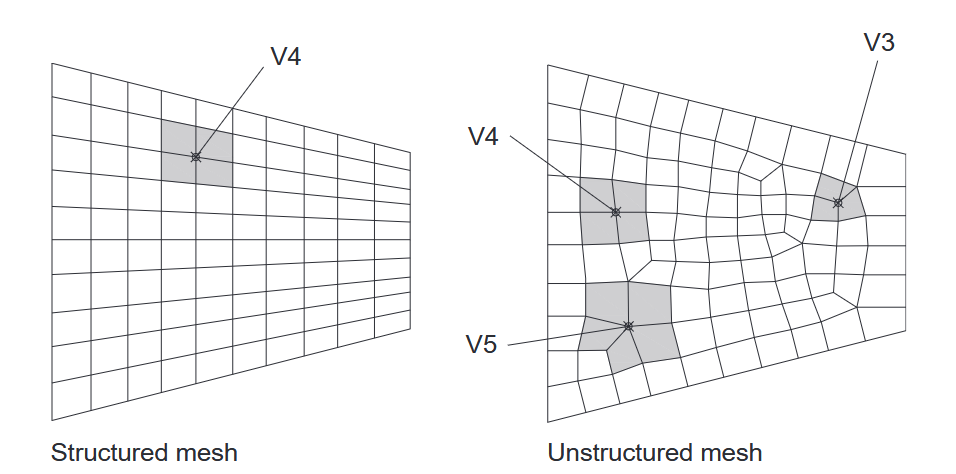
图片取自：Metal Forming Formability, Simulation, and Tool Design (Chris V. Nielsen, Paulo A.F. Martins)

按网格类型分类

  • 点集网格（Point Set Mesh）：由离散点组成，通常不包含连接信息，适用于点云数据处理。
  • 面片网格（Surface Mesh）：网格单元仅限物体表面，常见类型有三角形面片网格和四边形面片网格。
  • 体积网格（Volume Mesh）：由三维单元组成，适用于三维问题，常见类型有四面体网格和六面体网格。

按网格的适应性分类

  • 均匀网格（Uniform Mesh）：网格单元大小一致，适用于简单几何问题。
  • 自适应网格（Adaptive Mesh）：网格密度根据计算需求动态调整，适用于精细模拟高梯度区域。

按网格的质量分类

  • 高质量网格（High-Quality Mesh）：网格单元形状规整，适用于高精度仿真。
  • 低质量网格（Low-Quality Mesh）：网格单元可能畸形，适用于快速仿真或低精度要求。

生成方法

chatgpt结果，先列上

网格生成算法 应用场景 特点
Delaunay 三角剖分 适用于二维空间的不规则区域 优化三角形形状，避免长而细的单元，生成高质量网格。
Voronoi 图 点集划分，常与Delaunay三角剖分结合使用 将空间分割为Voronoi区域，用于定义网格单元。
前沿推进法（Advancing Front） 生成不规则区域网格 从边界开始逐步生成单元，覆盖整个域。
八叉树/四叉树（Octree / Quadtree） 大规模计算、自适应网格生成 递归划分空间，适应复杂几何形状和动态变化。
拉普拉斯平滑（Laplacian Smoothing） 优化现有网格，改善网格质量 平滑节点位置，减少畸形单元，优化网格形状。
网格重构算法（Mesh Refinement） 自适应网格、网格细化或粗化 动态调整网格精度，特别适用于自适应网格。
多边形剖分（Polygonal Mesh Generation） 复杂几何形状的网格生成 生成多边形单元，适应更复杂的形状。
结构化网格生成（Structured Mesh Generation） 规则几何区域（如矩形、正方形） 生成规则网格单元，计算效率高，适用于简单几何问题。
自适应网格生成（Adaptive Mesh Refinement, AMR） 需要精细模拟高梯度区域或重要区域 根据精度要求动态调整网格密度，适合复杂现象模拟。
混合网格生成（Hybrid Mesh Generation） 同时处理规则和复杂区域的应用 结合结构化和非结构化网格的优点，适应多种几何形状。
六面体网格生成（Hexahedral Mesh Generation） 规则三维几何区域（如矩形、立方体） 生成六面体单元，适用于流体力学或结构分析中的高精度计算。
混合元素网格生成（Mixed-Element Mesh Generation） 复杂几何或多物理场仿真 结合多种网格元素（四面体、六面体、棱柱等），适应复杂场景。
网格划分法（Grid Generation by Partitioning） 将复杂几何域分割为多个规则子域 常用于流体动力学、热传导等领域，稳定且高效。

开源软件

gmsh

  • https://gmsh.info/
  • https://pypi.org/project/gmsh/
  • https://github.com/pyvista/scikit-gmsh

注意: 采用GPL协议

tetgen

  • https://wias-berlin.de/software/index.jsp?id=TetGen
  • https://github.com/ufz/tetgen
  • https://github.com/pyvista/tetgen

注意：采用 AGPL 协议！！

MeshFix

  • https://github.com/MarcoAttene/MeshFix-V2.1
  • https://github.com/pyvista/pymeshfix

注意：采用 GPL 协议

gmsh例子

gmsh

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import gmsh

# 初始化 GMSH
gmsh.initialize()

# 创建一个 2D 矩形
length = 10.0
height = 5.0

# 创建四个顶点
p1 = gmsh.model.geo.addPoint(0.0, 0.0, 0.0)
p2 = gmsh.model.geo.addPoint(length, 0.0, 0.0)
p3 = gmsh.model.geo.addPoint(length, height, 0.0)
p4 = gmsh.model.geo.addPoint(0.0, height, 0.0)

# 创建四条边
l1 = gmsh.model.geo.addLine(p1, p2)
l2 = gmsh.model.geo.addLine(p2, p3)
l3 = gmsh.model.geo.addLine(p3, p4)
l4 = gmsh.model.geo.addLine(p4, p1)

# 创建一个封闭的曲线环
loop = gmsh.model.geo.addCurveLoop([l1, l2, l3, l4])

# 创建一个面
surface = gmsh.model.geo.addPlaneSurface([loop])

# 生成网格
gmsh.model.geo.synchronize()
gmsh.model.mesh.generate(2)

# 保存网格为 .msh 文件
gmsh.write("rectangle.msh")

# 结束 GMSH
gmsh.finalize()

print("Mesh generation finished!")

可以用pyvista显示（可能不太对，太复杂了）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import meshio
import pyvista as pv

# 使用 meshio 读取 GMSH 生成的网格文件
mesh = meshio.read("rectangle.msh")

# 提取点（vertices）和三角形单元（triangles）
points = mesh.points
cells = mesh.cells_dict["triangle"]

cells_flat = cells.flatten()  # 展平为一维数组
n_cells = len(cells_flat) // 3  # 计算三角形单元的数量

# 构建单元数组：每个元素包含一个整数 3（表示每个单元为三角形），后跟三个顶点索引
cell_array = [[3, cells_flat[i], cells_flat[i+1], cells_flat[i+2]] for i in range(0, n_cells*3, 3)]

# 将点和单元传递给 PyVista 的 PolyData 对象
grid = pv.PolyData(points, cell_array)

# 可视化网格
plotter = pv.Plotter()
plotter.add_mesh(grid, show_edges=True, color="lightblue")
plotter.show()

参考

  • https://en.wikipedia.org/wiki/Mesh_generation
  • https://www.robertschneiders.de/meshgeneration/meshgeneration.html
  • https://github.com/nschloe/meshio

Posted by Debao Zhang Tools