电子束斑（探针）直径小记

几何与电子光学成像
像差（aberration）
束斑大小（Spot Size）
- 半张角
参考

几何与电子光学成像

在几何光学中，我们中学都做过透镜成像的试验（将蜡烛成像到像平面上）：

imaging

而在电子光学中，概念是类似的，通过各个静电透镜或/和磁透镜，将光源（电子枪枪尖）成像到样品表面上。

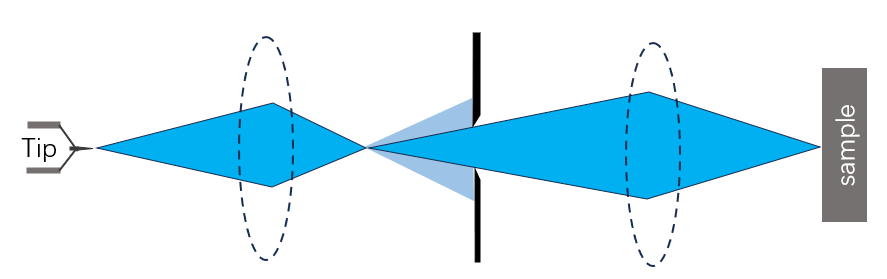
imaging

理想情况下，第一个汇聚透镜（枪镜）负责把物缩小，而第二个透镜（物镜）负责聚焦到样品表面（也承担也物缩小任务）。

但由于各种像差的存在，像的尺寸（Spot size，Probe diameter）比理想的高斯像要大。

为了让像点尽可能小（以提升分辨力），一方面追求更小的光源（枪尖直径），一方面致力于消除各种像差。

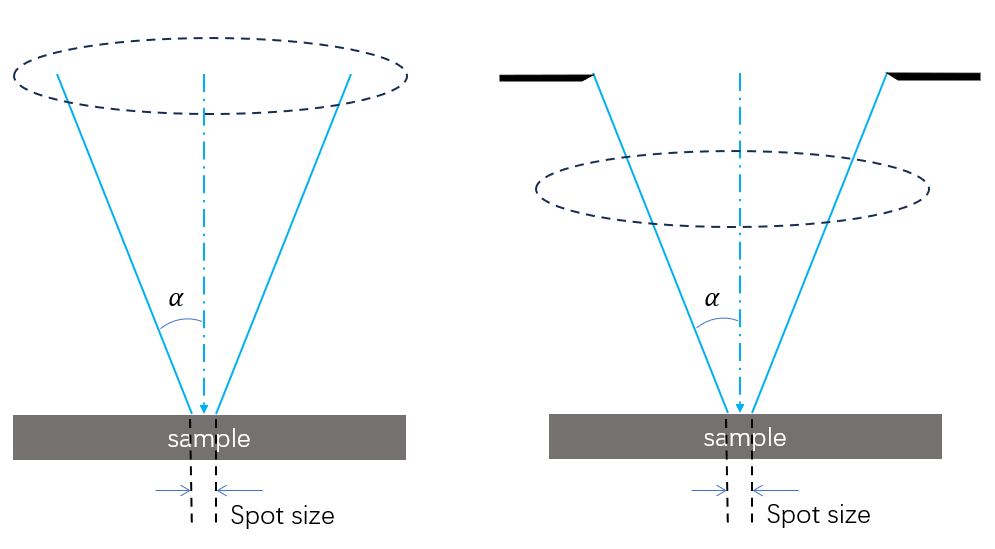
spot size

除了束斑大小（Spot Size，Probe Diameter）之外，一般还会关注：落点能量(Landing Energy，Accelerating Voltage)，束流大小(Probe Current，Beam Current)，半张角（Convergence Angle）。

像差（aberration）

像差（aberration）是电子光学系统中偏离理想成像的现象。在理想成像的情况下，从物体平面上某一点发出的所有电子束通过透镜后会在图像平面上汇聚到一个点。然而，在实际透镜中，这些电子束不会汇聚到单一的点，而是形成一个模糊的图像。像差可分为“几何像差”（geometrical aberrations）和“色差”（chromatic aberrations）。

几何像差取决于从物体平面发出的电子束的位置和角度，并可以表示为电子束与光轴的距离 𝑟 和电子束与光轴之间的角度 𝛼 的函数。在这些像差中，仅依赖于角度 𝛼 的像差被称为轴向几何像差（axial geometrical aberrations），而依赖于距离 𝑟 的像差则被称为非轴向几何像差（off-axial geometrical aberrations）。

色差（Chromatic Aberration）是在电子束没有单一能量而存在能量分布时产生的。也就是说，具有不同能量的电子束在通过电磁透镜时会发生不同角度的偏折，从而导致色差。

几何像差（Geometrical aberrations）

几何像差大致可分：赛德尔像差（Seidel Aberrations）和寄生像差（Parasitic Aberrations）。一般只关注赛德尔像差（Seidel Aberrations）。

赛德尔像差（Seidel Aberrations） 是指在几何光学中，由于透镜或光学系统的缺陷或不理想设计，导致的几种基础像差。这些像差是由德国物理学家 Karl Seidel 在19世纪提出的，用以描述透镜的光学误差。

像差类型	定义	影响
球差 (Spherical Aberration)	由于透镜形状不理想，光线聚焦点不同，导致模糊。	近轴和远轴光线聚焦位置不同，成像模糊。
彗差 (Coma)	离光轴较远的光线偏折过大，形成彗星尾状的模糊。	图像边缘模糊，并呈现“尾巴”状的拉伸。
像散 (Astigmatism)	透镜非对称导致在不同方向聚焦位置不同，产生变形。	图像沿某方向聚焦良好，另一方向则模糊，形状扭曲。
场曲 (Field Curvature)	焦平面呈曲面状，非平坦，导致图像不均匀。	离焦点较远的区域变形，成像不均匀。
桶形畸变 (Barrel Distortion)	图像边缘拉伸成桶形，中央正常。	边缘变形，视野边缘拉伸，尤其在大视野下明显。
枕形畸变 (Pincushion Distortion)	图像边缘向中心收缩，中央正常。	图像边缘拉拢，尤其在大视野放大时产生畸变。

这些像差中，球差是唯一轴上不等于零的几何像差，也就是轴向几何像差（axial geometrical aberrations），特别关注一下：

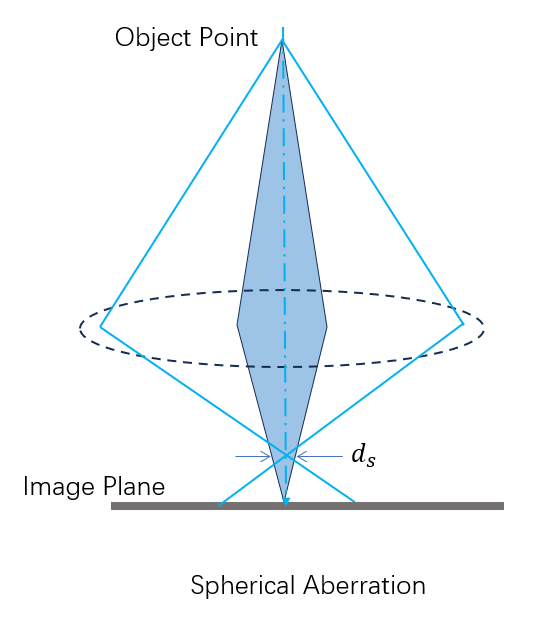
spherical_aberration

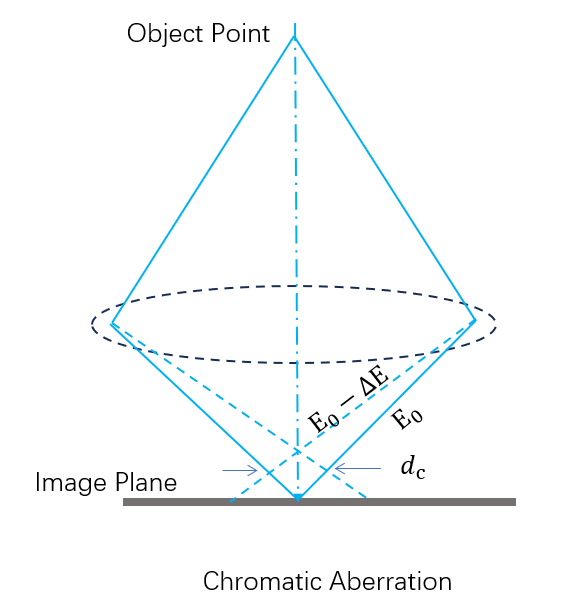
色差（Chromatic Aberration）

电子光学系统中的电子束具有不同的能量（即色散），在透镜中不同的电子能量会发生不同程度的偏折，导致不同能量的电子聚焦在不同的地方。

chromatic_aberration

衍射（Diffraction）

衍射像差（Diffraction Aberration）是指由衍射效应引起的图像失真。它与透镜设计缺陷不同，衍射像差是由于电子的波动性质导致的。

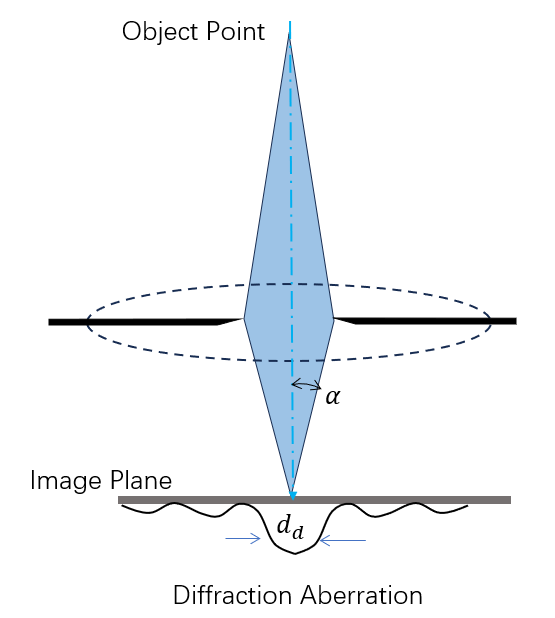
$diffraction_aberration$

束斑大小（Spot Size）

束斑大小（Spot Size）是指聚焦到样品表面的入射电子探针的直径。以下方程广泛用于定义束斑直径：

d = \sqrt{d_0^2 + d_d^2 + d_s^2 + d_c^2}

上述方程表示，在样品表面，束斑直径 d 由四个项的均方根值计算得出，即：

d_0 ：没有像差时由电子源获得的束斑直径
d_d ：由衍射像差决定的束斑直径
d_s ：由球差决定的最小模糊圆的束斑直径
d_c ：由色差决定的最小模糊圆的束斑直径

下方的方程则给出了 d_0 、 d_d 、 d_s 和 d_c 的具体描述：

d_0 = \bigg(\frac{2}{\pi\alpha}\sqrt{\frac{I_p}{\beta}}\,\bigg) \\ d_d = \frac{0.61\lambda}{\sin\alpha} \\ d_s = 0.5C_s\alpha^3 \\ d_c = C_c\frac{\Delta E}{E}\alpha

其中：

I_p 是探针电流
\beta 是电子枪的亮度
\alpha 是电子探针的聚焦半角
\lambda 是电子波长
C_s 是物镜的球差系数
C_c 是物镜的色差系数
E 是电子束的能量
\Delta E 是电子束的能量分布

半张角

上面方程表明，束斑大小 d 是半张角 \alpha 的函数：

d_0 、 d_d ：随 \alpha 增加而减小
d_s 、 d_c ：随 \alpha 增加而增加

这样一来，一味增大或一味地缩小都是有问题的。为了找到最佳的半张角，经常看到下面这样的图：

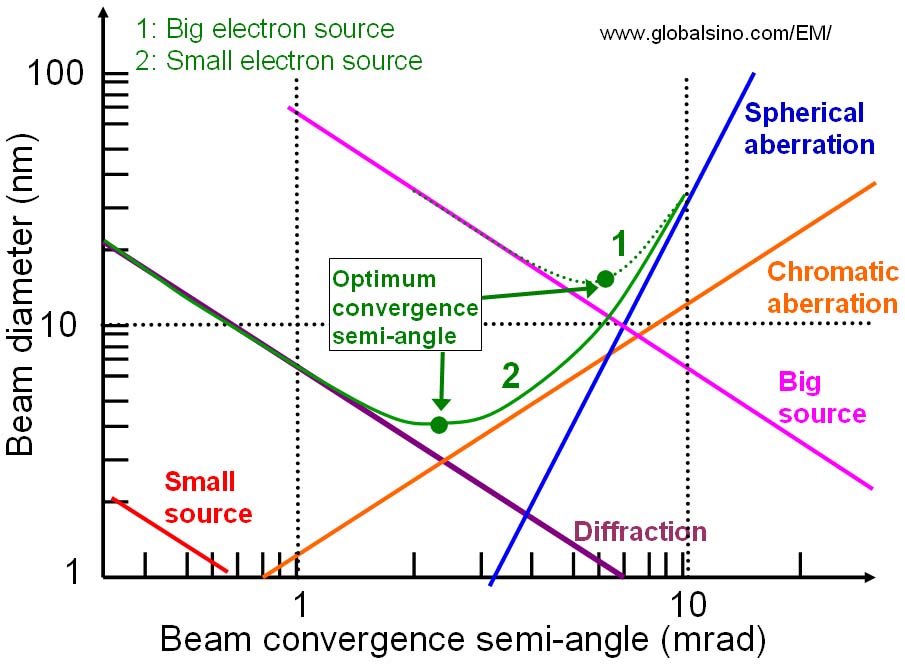
semi angle

图片来源：globalsino.com

注意： \alpha 的定义，不同资料给出的不同，有的强调是物点对透镜所张的孔径角，有的是像点到透镜的孔径角。

参考

https://www.jeol.com/words/semterms/20121024.063858.php
https://www.thermofisher.com/us/en/home/global/forms/industrial/spot-size-sem.html
https://www.jeol.com/words/emterms/20231204.php
https://www.jeol.com/words/emterms/20121023.035259.php
https://www.jeol.com/applications/pdf/sm/sem_atoz_all.pdf
https://www.globalsino.com/EM/page2749.html

1+1=10

记记笔记，放松一下...