1+1=10

记记笔记，放松一下...

电子光学基础：电子光学与光线光学相似性

接前面 电子光学基础：电子的速度与波长，继续看看...

和光子一样，电子也具有波粒二象性，而且电子的德布罗意波长一般很短，较少涉及到衍射、干涉等波动光学的内容，所以可以和光线光学（几何光学）的光线传播类比。

电子光学折射定律

几何光学是描述光束行程的。光线通过均匀的、各向同性的透明介质时是沿直线传播的，而当通过不均匀处，比如两种介质的交界面时，会产生反射和折射现象。如果我们把真空中的折射率取为1，则可以用相对折射率来表征光线通过的介质。

假设光线由折射率为 n_1 的介质通过交界面进入折射率为 n_2 的介质，按照斯涅尔定律（Snell's Law），有：

\frac{\sin \alpha_1}{\sin \alpha_2} = \frac{n_2}{n_1}

式中 \alpha_1 和 \alpha_2 分别是光线的入射角和折射角。n_1 和 n_2 则分别是对应介质的折射率。

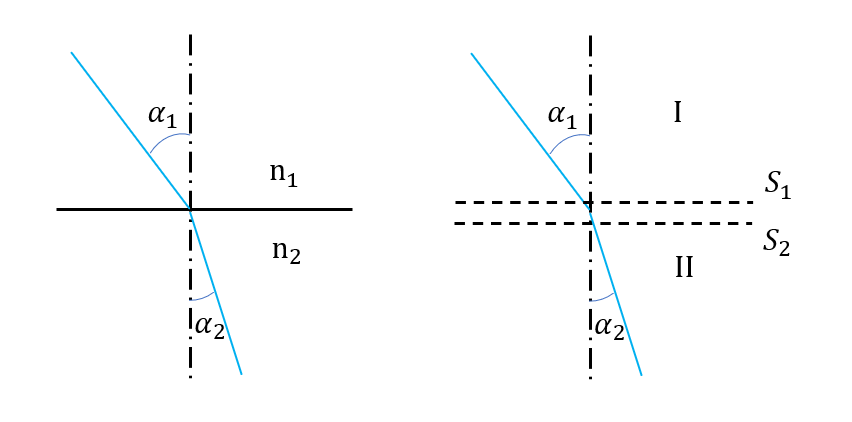
光线与电子的折射

现在考虑电子进入两个不同电位 U_1 和 U_2 空间的交界面 S_1 S_2 时的行为。设等电位区 I 和 等电位区 II 的电位分别为 U_1 和 U_2，且 U_1 > U_2，平面 S_1 和 S_2 之间的距离为 d，则平面间的电场强度为：

\mathbf{E} = \frac{U_2 - U_1}{d}

在等位空间 I 和 II 中，电位梯度为零；而在交界面 S_1 和 S_2 之间存在电场，且垂直于界面。因此，电子穿过这一空间时，其速度会收到影响。由于电场力垂直界面，所以电子只在界面的额法向方向上加速（或减速），而切向速度保持不变，即：

v_1\sin \alpha_1 = v_2 \sin \alpha_2

因而：

\frac{\sin \alpha_1}{\sin \alpha_2} = \frac{v_2}{v_1}

在非相对论情况下，当电子从初速、电位均为零的点开始运动，到达电位 U 处时，我们已知：

v = \sqrt{\frac{2 \lvert e \rvert U}{m_0}}

可得

\frac{\sin \alpha_1}{\sin \alpha_2} = \frac{\sqrt{U_2}}{\sqrt{U_1}}

与斯涅尔定律相比较，可知 \sqrt{U} 在电子光学中对应于几何光学中的折射率 n。该式子反映了电子在电场中的折射规律，称为 电子光学的折射定律。

研究表明，电子穿越磁场时，也发生折射。这时折射率和入射角有关，和磁场等效的折射率不仅是不均匀的，还是各向异性的。在电磁场存在时，非相对论下 折射率 具有下面的形式：

n = \sqrt{\frac{2 \lvert e \rvert U}{m_0}} + \frac{e}{m_0}\mathbf{A}\cdot\mathbf{s^0}

式中 \mathbf{A} 是矢量磁位，\mathbf{s^0} 是与轨迹相切的单位矢量。

其实，这个式子是通过对比电子在电磁场中运动的最小作用量原理（哈密顿原理）与几何光学中的费马原理的相似性得出。

费马原理与哈密顿原理

费马由于提出了光线传播的费马原理而称为现代几何光学的奠基人之一。费马原理从光程的观点来描述光传播的规律。它具有普遍的意义。

所谓光程（optical path)，是指光在介质中所经过的几何路程 l 与该介质折射率 n 乘积，相当于光在介质中走过 l 这段路程的时间 t 内，在真空中所走过的路程。

费马原理（Fermat's principle）：光从一点到另一点是沿光程（optical path）为极值的路径传播的。即光沿着光程为极小、极大或常量的路径传播。其数学表达式如下：

\delta \int_{P_0}^{P_1} n \mathrm{d}s = 0

受费马原理的最小化思想启发，莫培督、拉格朗日和哈密顿等路径最小化的思想逐步扩展到力学和到更广泛的物理学中，提出了哈密顿原理。

哈密顿原理（Hamilton's Principle）是经典力学中的一个基本变分原理。其核心是，物理系统从一个状态演化到另一个状态时，总是沿着使得作用量（action）极值的路径进行运动。 其数学表述为：

\delta S = \delta \int_{t_0}^{t_1} L \mathrm{d}t = 0

在经典力学中，作用量 S 被定义为拉格朗日量 L=T-V 在时间 t 上的积分，其中 T 为动能，V 为势能。在磁场与静电场存在境况下，对于以非相对论速度运动的粒子，其拉格朗日函数：

L = \frac{m_0v^2}{2} -e U + e\mathbf{A} \cdot v

尽管上面哈密顿原理的式子在力学中如此基本与简洁，但是在电子光学中直接应用并不多。因为带电粒子光学关系的是粒子运动的轨迹，各坐标随时间的变化关系尚属次要问题。所以，希望泛函积分中以空间坐标而不是以时间坐标为自变量。

\delta \int_{P_0}^{P_1}\bigg[\sqrt{\frac{2 \lvert e \rvert U}{m_0}} + \frac{e}{m_0}\mathbf{A}\cdot\mathbf{s^0}\bigg]\mathrm{d}s = 0

式中 P_0 及 P_1 为粒子开始 t_0 及结束 t_1 的坐标，\mathbf{s}^0 是与轨迹相切的单位矢量，即速度方向的单位矢量。

这个式子和费马原理就比较对称了。进而得到上一节提到的存在磁场时的电子光学折射率。

透镜术语与概念

电子光学从几何光学中借鉴的了大量的术语，所以也有透镜、焦面、主面、焦点、焦距、像差等概念。

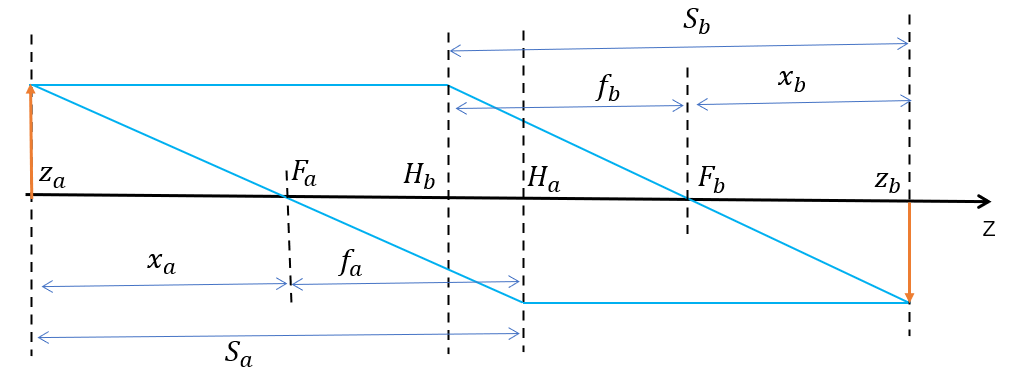
Image relationship

  • 基点 (Cardinal point)：光学系统中关键的几何点，通常包括主点、焦点等，用来描述物体与图像之间的关系。
    • 主点 (Principal point)：光学系统的一个参考点，通常位于透镜的光轴上，代表光学系统的虚拟或实际光源。
    • 焦点 (Focal point)：光学系统中的一个关键点，所有平行入射的光线会聚集或发散至焦点。
    • 节点 (Nodal point)：光学系统中一对特殊点，通过这些点的光线不会改变其方向，经过光学系统后，物体和图像位置保持几何相似。
  • 基面 (Cardinal plane)：与基点对应的平面，通常是主面和焦面等，用于描述光学系统的成像性质。
    • 主面 (Principal plane)：光学系统中的参考平面，包含光轴和主点，通常用于透镜系统的几何描述。
    • 焦面 (Focal plane)：与焦点平行并通过焦点的平面，所有聚焦的光线都位于此平面上。

对于旋转对称的薄透镜，先关注一下其焦距

静电透镜聚焦能力：

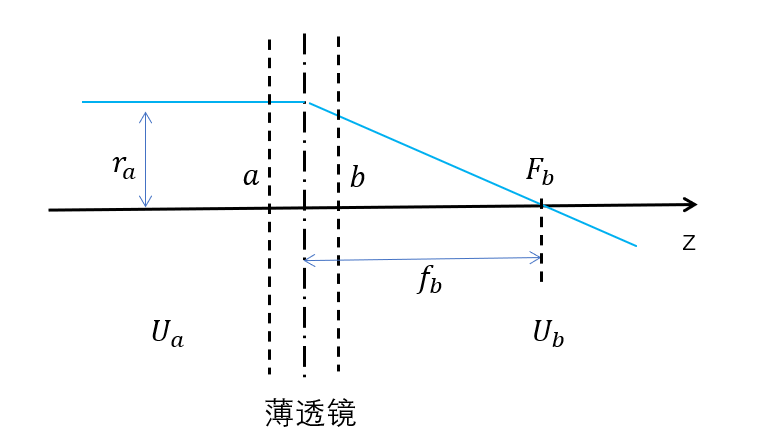
thin lens

轴对称电场对电子轨迹有聚焦成像的作用，成为之静电透镜。当透镜厚度（透镜场的作用范围）比焦距小的多时，可以近似看作物主面与像主面在透镜中心处重合，称为薄透镜。

\frac{1}{f_b} = \frac{1}{4}\frac{1}{\sqrt{U_0(z_b)}}\int_{z_a}^{z_b}\frac{U''_0(z)}{\sqrt{U_0(z)}}\mathrm{d}z

静电透镜的聚焦能力与带电粒子的电荷和质量无关，通用性强。不过考虑到强电场时容易引发击穿和放电等问题，对真空以及电极间绝缘要求高一些。

对上式，借助分部积分，小区二阶导，还可以写作：

\frac{1}{f_b} = \frac{1}{8}\frac{1}{\sqrt{U_0(z_b)}}\int_{z_a}^{z_b}\frac{U'^2_0(z)}{{U_0(z)}^{\frac{3}{2}}}\mathrm{d}z

注意：加速电压很大时，由于电极间电压受击穿限制又不能很大，静电透镜聚焦本领会急剧降低。所以对于高能带电粒子束，会使用非旋转对称的四极透镜。

磁透镜聚焦能力：

\frac{1}{f} = \frac{e}{m}\frac{1}{8U}\int_{-\infty}^{+\infty}\boldsymbol{B}_{0z}^2(z)\mathrm{d}z

带电粒子在磁场中受洛伦兹力下运动，远不如在电场下直观，所以磁透镜比较复杂：

  1. 磁透镜是聚焦透镜，无论线圈中电流方向如何
  2. 磁透镜会聚能力与轴上磁场积分成正比，磁场越强，会聚能力越强
  3. 磁透镜的聚焦能力与电压成反比，带电粒子轴向速度越快，受力时间越短，聚焦能力越弱
  4. 磁透镜的聚焦能力与带电粒子的荷质比有关。质量越大，聚焦力越弱。
  5. 磁透镜存在像转角，它与线圈中电流方向有关。

正由于磁透镜这种性质，使得其对于远比电子质量重的离子，聚焦能力变得很弱。所以离子光学中，不使用磁透镜。

另外，注意到U增大时，其聚焦本领也会迅速变小，而轴上磁场受磁饱和限制也不能很大，所以对于高能带电粒子束，磁透镜也不好使。

与几何光学主要差异

尽管有电子与光线有一定的相似性，但是，也有很大不同

  • 电位 U 空间中是连续的，不同于几何光学可以在交界面上突变。
  • 电位 U 分布符合泊松方程，等位面到处相关，不同于几何光学可以对透镜表面进行局部修正或任意组合以减少像差。
  • 电位 \sqrt{U} 的数值可以自由调节，且调整范围很大，不同于几何光学中折射率由材料决定，且受介质天然性质限制（可见光段不超过2.5，红外段不超过5）。
  • 有磁场存在时，电子光学折射率是非均匀的和各向异性的，不同于几何光学中的光线可逆。
  • 电子之间存在相互作用的排斥力（空间电荷效应），在强流是必须考虑，这在几何光学中的光子中是不存在的。

Posted by Debao Zhang SEM