蒙特卡洛模拟小记

蒙特卡洛模拟(Monte Carlo simulation)的名称来自摩纳哥的蒙特卡洛赌场，因为模拟过程中使用了大量随机数，类似于赌博中的随机性。这种命名由美国数学家斯坦尼斯拉夫·乌拉姆（Stanislaw Ulam）和约翰·冯·诺依曼（John von Neumann）【就是提出冯·诺依曼结构的那个现在计算机之父】等人提出。

什么是蒙特卡洛模拟?

蒙特卡洛模拟是一种计算方法，通过大量的随机抽样和概率统计来解决复杂问题。我们可以把它想象成一个不断“投骰子”的过程。每次投掷都得到不同的结果，通过多次重复，可以得出系统行为的可能性分布。这个过程让我们能够对系统的不确定性进行更细致的分析，最终获得可能的结果范围。

蒙特卡洛模拟在20世纪40年代的曼哈顿计划中得到系统发展，当时科学家们需要模拟原子粒子的运动，这种运动充满随机性。

基本步骤

尽管听起来很复杂,不过其过程相对直接。蒙特卡洛方法的主要步骤：

定义问题和模型：明确问题，把它转化为数学模型，包含随机变量。
确定输入的概率分布：定义模型中的不确定变量并给出其概率分布（如正态分布、三角形分布等）。
生成随机样本：利用计算机生成大量随机数，为每个随机变量创建大量可能的输入组合。
运行模拟：将每一组随机样本代入模型进行计算，重复该过程数百甚至数千次。
分析结果：收集所有模拟结果，计算出变量的分布情况、期望值、方差等统计数据，从而推测出不同结果的概率。

用两个小例子看下步骤

计算圆周率

似乎大家都喜欢用蒙特卡洛方法计算圆周率。

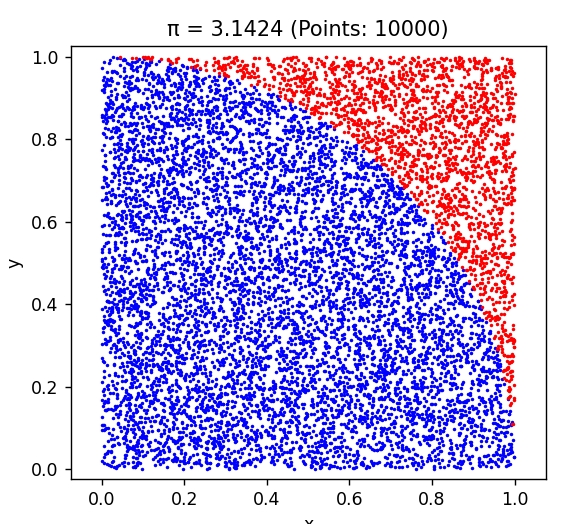
monte carlo method pi

想象一个正方形中，内嵌一个与其边长相同的四分之一圆弧。假设该正方形的边长为 1，那么：

四分之一圆的面积为 π/4
正方形的面积为 1

因此，四分之一圆面积占正方形面积的比例为 π/4。具体步骤：

生成随机点：在正方形中随机生成大量的点，每个点的 x 和 y 坐标在 0 到 1 之间。
判断是否在圆内：对于每个点，计算其到圆心 (0,0)的距离。
计算比例：统计所有点中落在圆内的比例。
估算 π：通过该比例乘以 4 来得到 π 的近似值。

简单的python代码如下：

import random
import matplotlib.pyplot as plt

def estimate_pi(num_points):
    inside_circle = 0
    points_inside_x, points_inside_y = [], []
    points_outside_x, points_outside_y = [], []

    for _ in range(num_points):
        x, y = random.random(), random.random() # Generate a random point
        if x**2 + y**2 <= 1:  # Check if point is inside the circle
            inside_circle += 1
            points_inside_x.append(x)
            points_inside_y.append(y)
        else:
            points_outside_x.append(x)
            points_outside_y.append(y)

    pi_estimate = (inside_circle / num_points) * 4
    return pi_estimate, points_inside_x, points_inside_y, points_outside_x, points_outside_y

#-----------------

# Set the number of points
num_points = 10000
pi_estimate, points_inside_x, points_inside_y, points_outside_x, points_outside_y = estimate_pi(num_points)

# Plot the results
plt.figure(figsize=(6, 6))
plt.scatter(points_inside_x, points_inside_y, color="blue", s=1, label="Inside")
plt.scatter(points_outside_x, points_outside_y, color="red", s=1, label="Outside")
plt.title(f"π = {pi_estimate:.4f} (Points: {num_points})")
plt.axis("equal")
plt.show()

计算多重积分

I = \int_0^1\int_0^1\int_0^1 (x + y^2 + z^3) dxdydz

使用蒙特卡罗方法来估算这个积分，遵循以下步骤：

在立方体内随机生成 N 个点。
计算每个点的函数值 f(x,y,z)。
取这些函数值的平均值，并乘以立方体的体积（此处为1），得到积分的近似值。

import numpy as np

def f(x, y, z):
    return x + y**2 + z**3

def monte_carlo_integration(num_samples):
    # 随机生成 num_samples 个点
    x = np.random.uniform(0, 1, num_samples)
    y = np.random.uniform(0, 1, num_samples)
    z = np.random.uniform(0, 1, num_samples)

    # 计算每个点的函数值
    function_values = f(x, y, z)

    # 计算积分的近似值
    integral_estimate = np.mean(function_values)

    return integral_estimate

# 设置样本数量
num_samples = 100000
result = monte_carlo_integration(num_samples)

print(result)

某次结果如下：

1	`1.0834714194252095`

可以和解析值（1+1/2+1/3 = 1.08333...）比较。

应用

蒙特卡洛模拟应用广泛，几乎可以应用于任何含有不确定性的问题，比如：

物理学和工程：用于核物理、材料科学、粒子物理的模拟。
金融：应用于股票价格预测、期权定价等。
项目管理：用于风险分析，进度预测等
计算生物学：用于分子模拟和基因表达研究。
医学物理：用于辐射治疗剂量计算和医疗影像分析。

在电子显微镜和X射线分析中，通过蒙特卡洛模拟来研究电子束与样品之间的相互作用。在电子显微镜中,空间电荷效应(Boersch效应)一般也通过蒙特卡洛方法进行数值模拟.

软件

先简单罗列

Github也能搜到不少,但都挺小众...

Geant4

https://geant4.org/
https://gitlab.cern.ch/geant4/geant4

Geant4（GEometry ANd Tracking）是一个使用蒙特卡洛方法模拟“粒子穿过物质的过程”的平台。

功能：

Geometry 是对实验物理布局的分析，包括探测器、吸收体等，考虑这些布局如何影响粒子在实验中的路径。
Tracking 是模拟粒子穿过物质的过程，涉及可能的相互作用和衰变过程。
Detector response 记录粒子通过探测器体积时的反应，并近似真实探测器的响应。
Run management 记录每次运行（即一组事件）的详细信息，并在不同运行之间设置实验的不同配置。

PENELOPE

http://www.oecd-nea.org/tools/abstract/detail/nea-1525

PENELOPE（PENetration and Energy LOss of Positrons and Electrons …and photons）是一款通用蒙特卡洛子程序包，用于模拟任意几何结构中的电子-光子耦合传输。该软件通过蒙特卡洛方法对正电子、电子和光子的穿透和能量损失进行精确建模，适用于多种科学和工程应用场景。

EGSnrc

https://github.com/nrc-cnrc/EGSnrc

EGSnrc（Electron Gamma Shower, National Research Council），发音 "eggs-N-R-C"。

EGSnrc 是一个软件工具包，用于进行电离辐射通过物质的蒙特卡罗模拟。它模拟光子、电子和正电子在 1 keV 到 10 GeV 动能范围内在均匀材料中的传播。

EGSnrc 于 2000 年首次发布，是对原先在 1970 年代斯坦福线性加速器中心（SLAC）开发的Electron Gamma Shower（EGS）软件包的全面改进。

EGSnrc 的一个显著特点是，它在带电粒子运输方面进行了重要的改进，提供了更好的低能截面，并包含 egs++ 类库以建模复杂的几何形状和粒子源。

MC X-Ray

https://montecarlomodeling.mcgill.ca/software/mcxray/mcxray.html

MC X-Ray 是一款新的蒙特卡洛模拟软件，是 Casino 和 Win X-Ray 程序的扩展版。它通过模拟不同几何结构的固体中的电子散射，计算完整的 X 射线光谱。

MC X-Ray 允许用户定义多达 256 个区域，这些区域可以是球体、圆柱体或水平与垂直平面的组合，每个区域都可以具有不同的成分。

MCXRay 被集成到 3D 处理平台 Dragonfly（加拿大蒙特利尔 ORS），其运行速度比原始程序快 100 到 1000 倍！

功能：

支持 3D 样品和复杂几何结构
明场、暗场、高角环形暗场检测器
3D 结果计算
显示电子轨迹
样品表面的电子与能量分布
透射电子分布
能量损失分布
X 射线光谱

Win X-Ray

https://montecarlomodeling.mcgill.ca/software/winxray/winxray.html

Win X-Ray 是一款蒙特卡洛模拟程序，用于模拟固体中的电子轨迹。Ray 是一款新的蒙特卡洛模拟扩展程序，基于知名的 CASINO 程序，它增加了回散电子、吸收电子、能量损失和 X 射线 φρz 曲线的统计分布。Ray 的新增功能包括完整的 X 射线光谱模拟和绝缘样品的电荷效应。

功能：

显示电子轨迹
回散电子分布
吸收电子分布
能量损失分布
特征 X 射线
制动辐射 X 射线
X 射线光谱
可模拟非导电样品

CASINO

Casino，发音 /kəˈsiːnəʊ/，原意是赌场的意思。这儿是刻意缩写。

CASINO（"monte CArlo SImulation of electroN trajectory in sOlids"）是全球知名的电子轨迹蒙特卡洛模拟程序。由 Prof. Gauvin 和他的研究生（Pierre Hovington 和 Dominique Drouin）在 Sherbrooke 大学最初开发。此后，该程序一直由 Sherbrooke 大学的 Dominique Drouin 和来自 Hydro-Québec 研究所（IREQ）的 Hendrix Demers 维护并改进。

不过软件似乎太老了，开发也不活跃，官网都已经无法访问。

它的2.4和3.3 两个版本差异很大。后者支持3D功能，但有人只使用它的2系列。

功能：

显示电子轨迹
回散电子分布
吸收电子分布
能量分布
φρz 曲线
快速模拟
回散和透射电子的角度检测器
复杂的光束参数
复杂几何结构
二次电子生成

SRIM/TRIM

http://www.srim.org/

SRIM（Stopping and Range of Ions in Matter）/ TRIM 是一款免费的蒙特卡洛模拟软件包，用于模拟固体中离子的轨迹。该程序能够计算离子的阻止本领和范围，被广泛应用于材料科学和辐照研究等领域。

Hurricane

http://www.samx.com/

SAMx 免费向社区提供蒙特卡洛程序 Hurricane。该软件包旨在基于蒙特卡洛方法模拟材料中的电子轨迹。Hurricane 拥有多种功能，特别的特点包括：

对弹性和非弹性相互作用的个别处理，无任何近似
支持矩阵中的多个成分
支持所有几何形状的模拟样品：
- 大块样品
- 基底上的薄膜
- 垂直界面的多个成分
- 由颗粒组成的矩阵样品
- 粗糙样品
存储所有计算参数，包括发射强度。

商业软件

BIOVIA Materials Studio：达索公司（Dassault Systèmes）
COMSOL Multiphysics：COMSOL
ANSYS：ANSYS
Mocasim：Silvaco
...

参考

https://en.wikipedia.org/wiki/Monte_Carlo_method
https://en.wikipedia.org/wiki/Geant4
https://www.memrg.com/programs-download
https://montecarlomodeling.mcgill.ca/links/Links_mcprgs.html
https://www.lehigh.edu/~maw3/link/mssoft/mcsim.html
https://www.microbeamanalysis.eu/links-resources

1+1=10

记记笔记，放松一下...