集合、群、环、域、空间等都是什么鬼？

查查资料，梳理一下

如果一个集合具有一种或几种代数运算，并满足若干运算法则（公理），则称为一个代数结构（Algebraic Structure）。群、环、域和向量空间都是代数结构。集合不是代数结构，但它是构建代数结构的基础。拓扑空间是几何结构而不是代数结构。

集合 (Set)：由德国数学家 康托尔 (Georg Cantor) 在19世纪末提出，集合论奠定了现代数学的基础。
群 (Group)：由法国数学家 伽罗瓦 (Évariste Galois) 在19世纪初引入，起源于代数方程对称性的研究。
环 (Ring)：由19世纪的数论研究发展而来，戴德金 (Richard Dedekind) 和 克罗内克 (Leopold Kronecker) 等人推动了环论的发展。
域 (Field)：伽罗瓦(Évariste Galois) 和 阿贝尔 (Niels Henrik Abel) 在19世纪通过解决代数方程的根问题扩展了域的理论。
空间 (Space)：赫尔穆特·哈斯 (Hermann Grassmann) 在19世纪提出向量空间，后由 希尔伯特 (David Hilbert) 推广，应用于量子力学和泛函分析。

空间名称	符号表示	说明	所属空间种类
欧几里得空间	ℝⁿ	具有 n 个实数坐标的向量空间，通常用于描述 n 维几何空间。	向量空间，度量空间
希尔伯特空间	𝐻 或 L²	带有内积的完备向量空间。常见的希尔伯特空间包括平方可积函数空间 L² 空间。	内积空间，巴拿赫空间
矩阵空间	𝑀ₘₓₙ	所有 m × n 维矩阵的集合。	向量空间
酉空间	ℂⁿ 或 𝐻ₘ	复数向量空间，配备复数内积，满足酉变换的条件。	内积空间，希尔伯特空间
辛空间	ℝ²ⁿ	一个偶数维的实向量空间，配备辛形式。通常描述物理系统中的相空间。	辛几何，向量空间
拓扑空间	(𝑋, τ)	一个集合 𝑋 和一个拓扑 τ 的组合，定义了开集和闭集的结构。	拓扑空间
度量空间	(𝑋, 𝑑)	一个集合 𝑋 和一个度量 𝑑 的组合，定义了元素之间的距离。	度量空间
巴拿赫空间	𝐵 或 Lᵖ	一个带有范数的完备向量空间。Lᵖ 空间是常见的巴拿赫空间，表示可测函数的某种范数可积空间。	范数空间，巴拿赫空间
范数空间	(𝑉, ∥·∥)	配备了范数 ∥·∥ 的向量空间，用于测量向量的大小。	范数空间
向量空间	𝑉	具有向量加法和标量乘法运算的向量集合。	向量空间
射影空间	ℙⁿ	n 维射影空间，表示所有非零向量的集合，按比例关系进行分组。	射影空间
李群	𝐺	既是群又是流形的结构，通常用于描述连续对称性。	拓扑群，流形，李群
张量积空间	𝑉 ⊗ 𝑊	两个向量空间 𝑉 和 𝑊 的张量积，表示两个空间的组合，用于多线性代数中。	向量空间
外积空间	Λᵏ 𝑉	向量空间 𝑉 的 k 次外积，通常用于描述几何和物理中的体积和面积等概念。	向量空间
函数空间	𝐶(𝑋) 或 Lᵖ(𝑋)	定义在集合 𝑋 上的函数的空间。𝐶(𝑋) 表示连续函数空间，Lᵖ(𝑋) 表示 p 次可积函数空间。	函数空间，巴拿赫空间

集合（Set)

集合（set）可以被定义为一组对象的集合，这些对象可以是任何东西，从数字、字母、点、线，到更抽象的概念。集合中的对象称为元素（element）或成员（member）。

表示法

集合有多种表示法

列举法（Roster or Tabular Form)

直接将集合的所有元素写在一对大括号 {} 里面，元素之间用逗号分隔。比如

集合 A={1,2,3,4,5}
集合 B={苹果,香蕉,桔子}

描述法（Set-builder Noation）

用一个条件来描述集合中的元素，而不是一一列出它们

A={x∣x 是大于0且小于6的整数}
B={x∣x 是奇数且 x<10}

符号表示法

常见的集合，有一些约定俗称的符号

ℕ — 自然数集合 (Set of Natural Numbers)
ℤ — 整数集合 (Set of Integers)
ℚ — 有理数集合 (Set of Rational Numbers)
ℝ — 实数集合 (Set of Real Numbers)
ℂ — 复数集合 (Set of Complex Numbers)
ℤ⁺ — 正整数集合 (Set of Positive Integers)
ℕ₀ — 非负整数集合 (Set of Non-negative Integers)
∅ — 空集 (Empty Set)
𝒫(A) — 幂集 (Power Set)

幂集（Power Set）是指某个集合的所有子集组成的集合。换句话说，给定一个集合 A，它的幂集 𝒫(A) 包含了A 的所有可能的子集，包括空集和集合本身。比如 A={1,2}，那么 𝒫(A)={∅,{1},{2},{1,2}} 。

集合性质

符号	名称 (Name)	定义 (Definition)
∈	属于 (Element of)	如果元素 x 属于集合 A，则记作 x ∈ A。
∉	不属于 (Not an element of)	如果元素 x 不属于集合 A，则记作 x ∉ A。
⊆	子集 (Subset)	如果集合 A 的所有元素都属于集合 B，则记作 A ⊆ B。
⊂	真子集 (Proper Subset)	如果集合 A 是集合 B 的子集且 A ≠ B，则记作 A ⊂ B。
⊇	包含 (Superset)	如果集合 A 包含集合 B 的所有元素，则记作 A ⊇ B。
⊃	真包含 (Proper Superset)	如果集合 A 真包含集合 B，且 A ≠ B，则记作 A ⊃ B。
∪	并集 (Union)	集合 A 和 B 的并集是 A ∪ B，包含 A 和 B 的所有元素。
∩	交集 (Intersection)	集合 A 和 B 的交集是 A ∩ B，包含 A 和 B 的共同元素。
∖或-	差集 (Difference)	集合 A 和 B 的差集是 A ∖ B，包含属于 A 但不属于 B 的元素。
𝐴ᶜ 或 𝐴̅	补集 (Complement)	集合 A 的补集是 Aᶜ 或 A̅，包含全集中不属于 A 的元素。

基数（Cardinal Number）/势（Cardinality）

势（Cardinality）用来表示某个集合的大小或元素的个数。记作 |A| 或 card(A)。它不仅适用于有限集合，也适用于无限集合。

初次看到这个势这个术语时是蒙的，它受日文翻译影响。

有限集合

对于有限集合，基数就是集合中元素的数量。

若 A = {1, 2, 3}，则 |A| = 3 。
若 B = {a, b, c, d, e} ，则 |B| = 5 。
若 C = ∅ （空集），则 |C| = 0 。

无限集合

对于无限集合，基数可以分为两类：

可数无限集（Countably Infinite Set）：这些集合的基数与自然数集 ℕ 的基数相同，记作 ℵ₀（读作“阿列夫零”）。
不可数无限集（Uncountably Infinite Set）：这些集合的基数比自然数集大，例如实数集 ℝ 的基数，通常记作 𝔠 或 2^ℵ₀，表示连续统的基数。

群（Group)、环（Ring）、域（Field）

先列个表格：

结构	运算数量 Num	运算符 Operator	元素 Element	主要性质 Structure
群 Group	1	o1 (加法/乘法)	单位元, 有逆	封闭性, 结合律
环 Ring	2	o1 (加法), o2 (乘法)	加法单位元, 加法有逆	加法为阿贝尔群,`乘法封闭, 结合律,`分配律
域 Field	2	o1 (加法), o2 (乘法)	加法单位元, 加法有逆，`乘法单位元, 乘法有逆 \| 加法为阿贝尔群,`乘法为阿贝尔群 (0 除外), ``分配律

再对照一下：在数系范围内

最小的数域是有理数域
最大的数域是复数域
自然数都构不成一个群，只能是半群、幺半群。

数系	符号	所属代数结构
自然数	ℕ	半群（Semigroup），幺半群（Monoid）
整数	ℤ	群（Group），环（Ring）
有理数	ℚ	群（Group），环（Ring），域（Field）
实数	ℝ	群（Group），环（Ring），域（Field）
复数	ℂ	群（Group），环（Ring），域（Field）

群（Group）

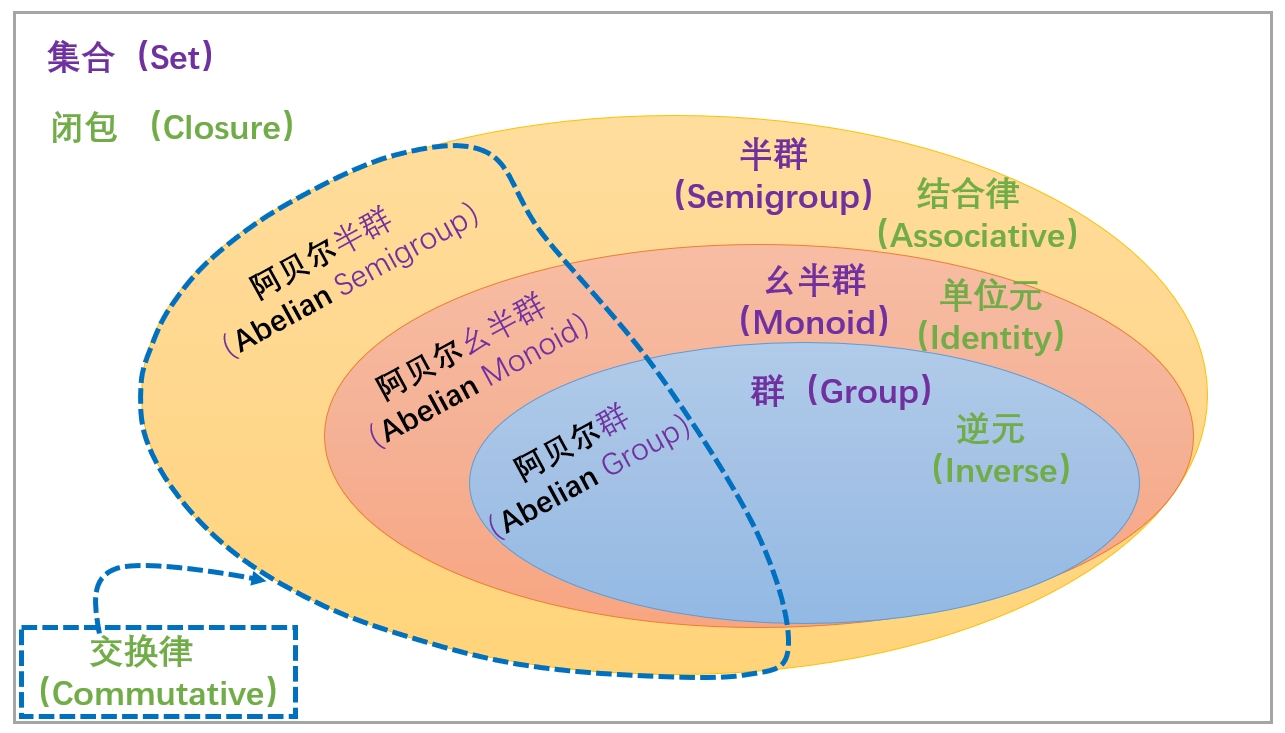
group

定义

一个群（Group）是由一个集合（Set）和一个二元运算（Binary Operation）组成的代数结构，它满足以下四个条件：

封闭性（Closure）：对于任意 a, b ∈ G，有 a ∘ b ∈ G。
结合律（Associativity）：对于任意 a, b, c ∈ G，有 (a ∘ b) ∘ c = a ∘ (b ∘ c)。
单位元（Identity Element）：存在一个元素 e ∈ G，使得对任意 a ∈ G，有 e ∘ a = a ∘ e = a。
逆元（Inverse Element）：对于任意 a ∈ G，存在一个元素 b ∈ G，使得 a ∘ b = b ∘ a = e。

如果群的运算还满足交换律（Commutativity，即 a ∘ b = b ∘ a），则称为阿贝尔群（Abelian Group）。

群、半群、幺半群

半群（Semigroup）：集合上的二元运算满足结合律，没有单位元或逆元的要求。
幺半群（Monoid）：是一个包含单位元的半群，但不要求每个元素有逆元。
群（Group）：不仅有单位元，而且每个元素都有逆元。如果二元运算满足交换律，则称为阿贝尔群（Abelian Group）。

性质	半群（Semigroup）	幺半群（Monoid）	群（Group）
集合	一个集合 S	一个集合 M	一个集合 G
二元运算	定义在 S 上的二元运算	定义在 M 上的二元运算	定义在 G 上的二元运算
结合律	满足结合律	满足结合律	满足结合律
单位元	不要求存在单位元	存在单位元	存在单位元
逆元	不要求存在逆元	不要求存在逆元	每个元素都有逆元
交换律	不要求	不要求	如果满足交换律，则为阿贝尔群

李群

得名于挪威数学家索菲斯·李（Sophus Lie，1842-1899）。

李群（Lie Group）是一个结合了群的代数结构和光滑流形的几何结构的数学对象，李群特别擅长描述连续对称性。

一些李群的例子？

群类型	符号	定义	特点	应用
一般线性群 (General Linear Group)	GL(n, ℝ) 或 GL(n, ℂ)	所有 n \times n 的可逆矩阵组成的群，运算是矩阵乘法。	非交换李群，描述一般线性变换。	线性代数、物理中的变换理论、控制论。
特殊线性群 (Special Linear Group)	SL(n, ℝ) 或 SL(n, ℂ)	所有行列式为 1 的 n \times n 可逆矩阵组成的群。	非交换李群，描述体积保持的线性变换。	物理学（守恒定律）、几何学、量子场论。
正交群 (Orthogonal Group)	O(n)	所有保持欧几里得距离不变的 n \times n 矩阵（正交矩阵）组成的群。	非交换李群，包含旋转和反射。	物理学（对称性）、计算机图形学、信号处理。
特殊正交群 (Special Orthogonal Group)	SO(n)	所有保持距离且行列式为 1 的 n \times n 正交矩阵（纯旋转）。	非交换李群，描述纯旋转。	物理学（旋转对称性）、计算机图形学、航天航空。
酉群 (Unitary Group)	U(n)	所有保持复数内积的 n \times n 酉矩阵组成的群。	非交换李群，描述复数空间中的对称性。	量子力学、量子信息、随机矩阵理论。
特殊酉群 (Special Unitary Group)	SU(n)	所有行列式为 1 的 n \times n 酉矩阵组成的群。	非交换李群，描述复数空间中的体积保持变换。	量子力学（自旋对称性）、粒子物理、规范场论。
洛伦兹群 (Lorentz Group)	O(1, 3)	保持狭义相对论时空距离不变的变换群。	非交换李群，描述空间和时间的对称性。	狭义相对论、量子场论、广义相对论。
庞加莱群 (Poincaré Group)	—	洛伦兹群和平移群的半直积，描述四维时空中的对称变换。	非交换李群，包含空间转动、时间平移等。	相对论物理学、量子场论、粒子物理。
圆周群 (Circle Group)	U(1)	所有单位模的复数组成的群，运算是复数乘法。	交换李群，描述一维复数向量的相位旋转。	电磁学、量子力学（U(1) 规范对称性）。
三维特殊酉群 (Special Unitary Group in 3D)	SU(3)	所有行列式为 1 的 3 × 3 酉矩阵组成的群。	非交换李群，描述三维复数空间中的对称性。	粒子物理学（强相互作用，量子色动力学）。
仿射群 (Affine Group)	Aff(n)	由 n -维空间的线性变换和平移组成的群。	非交换李群，描述线性变换和平移。	计算机视觉、几何学、机器人学。

如何直观理解？

旋转：假设你在二维平面上旋转一个物体。所有可能的旋转可以形成一个连续的对称性群，即李群。你可以通过一个连续的角度来描述旋转，比如从0度开始逐渐增加到360度，然后再回到原点。这种旋转形成了一个李群，通常记作 SO(2)，表示二维空间中的旋转群。
平移：类似地，在一条直线上任意移动一个物体，所有可能的平移也组成了一个李群。你可以通过平移的距离来描述对称性，这种李群通常记作 R，即实数在加法下形成的群。

非李群例子？

先找一些内容放上，以后再说

群类型	符号	定义	特点	应用
对称群 (Symmetric Group)	Sₙ	n 个元素的全排列构成的群，运算是排列的复合。	非交换群（当 n ≥ 3 时）。	化学（分子对称性）、物理学、组合数学。
二面体群 (Dihedral Group)	Dₙ	描述正 n 边形的旋转和反射的对称群。	非交换群，具有 2n 个元素。	图像处理、晶体学、机器人学。
阿贝尔群 (Abelian Group)	ℤ, +	满足交换律的群，如整数加法群。	交换群，但通常没有乘法结构。	密码学（ECC）、网络编码、物理学（守恒定律）。
有限循环群 (Finite Cyclic Group)	ℤₙ	由一个生成元生成的有限阶交换群。	交换群，通常没有加法结构。	密码学（Diffie-Hellman）、编码理论、图像处理。
四元数群 (Quaternion Group)	Q₈	包含 8 个元素的非交换群，元素有 {1, -1, i, -i, j, -j, k, -k} 。	非交换有限群，没有加法结构。	计算机图形学（旋转）、物理学（自旋）、控制理论。

环（Ring）

环（Ring）是一个代数结构，其中加法部分形成一个阿贝尔群，乘法部分满足封闭性、结合律和分配律。

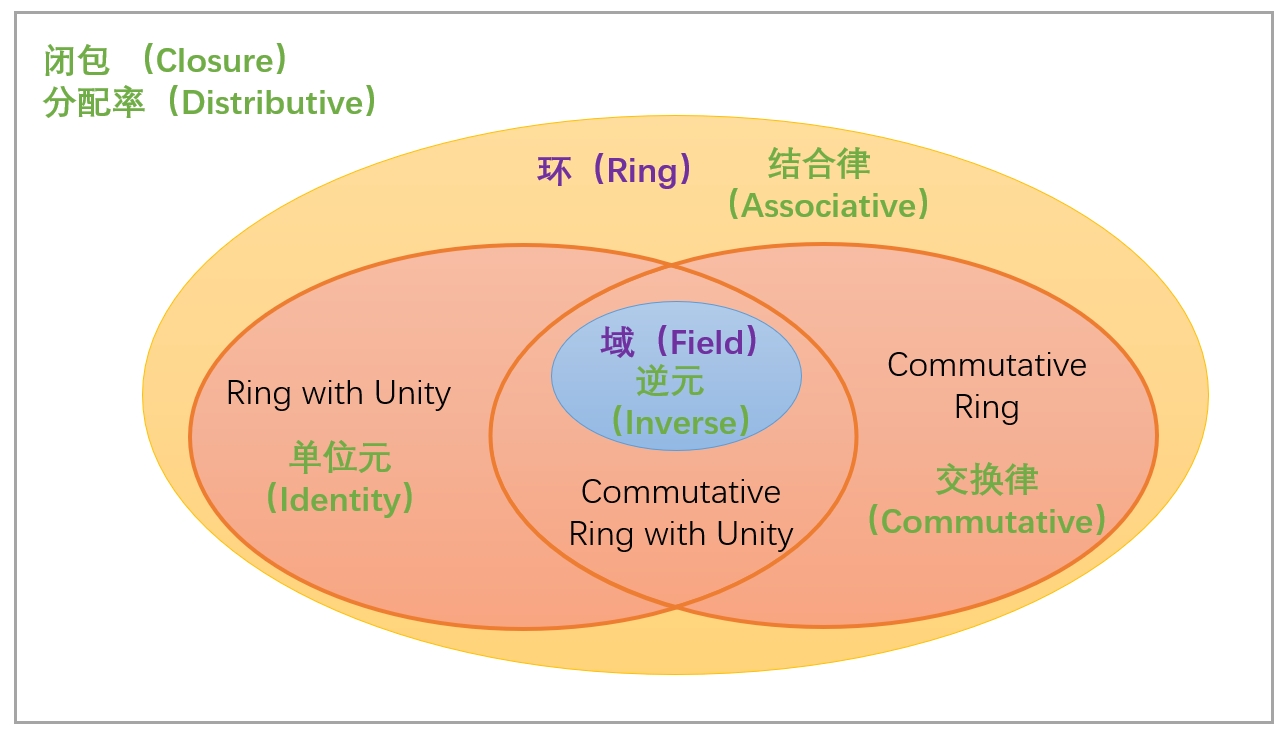
ring and field

定义

一个环（Ring）是由一个集合（Set）和两个二元运算（Binary Operations）——加法和乘法组成的代数结构，它满足以下条件：

加法部分：形成阿贝尔群（Additive Group）：

加法封闭性（Closure under Addition）：对于任意 a, b ∈ R，有 a + b ∈ R。
加法结合律（Associativity of Addition）：对于任意 a, b, c ∈ R，有 (a + b) + c = a + (b + c)。
加法交换律（Commutativity of Addition）：对于任意 a, b ∈ R，有 a + b = b + a。
加法单位元（Additive Identity）：存在一个元素 0 ∈ R，使得对任意 a ∈ R，有 a + 0 = 0 + a = a。
加法逆元（Additive Inverse）：对于任意 a ∈ R，存在一个元素 -a ∈ R，使得 a + (-a) = (-a) + a = 0。

乘法部分：

乘法封闭性（Closure under Multiplication）：对于任意 a, b ∈ R，有 a ∘ b ∈ R。
乘法结合律（Associativity of Multiplication）：对于任意 a, b, c ∈ R，有 (a ∘ b) ∘ c = a ∘ (b ∘ c)。

加法和乘法：

分配律（Distributivity）：对于任意 a, b, c ∈ R，有 a ∘ (b + c) = (a ∘ b) + (a ∘ c) 和 (a + b) ∘ c = (a ∘ c) + (b ∘ c)

注：

如果乘法也满足交换律（Commutativity of Multiplication），即对于所有 a, b ∈ R 有 a ∘ b = b ∘ a ，则称为交换环（Commutative Ring）。
如果 R 中存在一个乘法单位元 1 使得对所有 a ∈ R 有 1 ∘ a = a ∘ 1 = a，则称 R 为含幺环（Ring with Unity）。

环的例子？

环类型	符号	定义	特点	应用
整数环 (Integer Ring)	ℤ	包含所有整数，运算是通常的加法和乘法。	交换环，整除理论完善。	数论、同余、模运算、质数分解。
多项式环 (Polynomial Ring)	R[x]	由系数来自环 R 的多项式构成的环。	交换环，如果 R 是整环，则 R[x] 是唯一分解整环。	代数几何、计算机代数、控制理论。
矩阵环 (Matrix Ring)	Mₙ(R)	包含所有 n × n 矩阵的集合，矩阵的元素来自环 R。	非交换环，矩阵乘法不满足交换律。	线性代数、量子力学、控制理论、图像处理。
高斯整数环 (Gaussian Integer Ring)	ℤ[i]	由形如 a + bi 的复数构成，其中 a 和 b 是整数，i 是虚数单位。	交换环，但不是域，没有乘法逆元。	数论，特别是二次形式、素数分解。
模 n 环 (Ring of Integers Modulo n)	ℤ/nℤ 或 ℤₙ	包含整数 0, 1, 2, ..., n-1，运算按模 n 进行。	有限环，n 为素数时是域，n 非素数时是环。	密码学、编码理论、数论、计算机科学。
欧几里得环 (Euclidean Ring)	多种符号	可以使用欧几里得算法计算最大公因数的环，例如 ℤ、R[x]。	交换环，可以定义“度量”或“大小”的概念。	数论、多项式环、代数几何。
唯一分解整环 (UFD, Unique Factorization Domain)	多种符号	元素可以唯一地分解为不可约元素的乘积，如 ℤ 和 R[x]。	交换环，类似素数分解的唯一分解性质。	代数几何、数论、代数拓扑。
余数环 (Quotient Ring)	R/I	通过在一个环 R 上对某个理想 I 进行商构造出的环。	交换或非交换，取决于母环 R 的性质。	理想结构、代数几何、模论。
布尔环 (Boolean Ring)	B	满足 a² = a 的环，所有元素的平方等于自身。	交换环，常用于逻辑和组合代数。	逻辑学、组合数学、数字电路设计。
幂零环 (Nilpotent Ring)	N	一个环中，存在某个正整数 k 使得所有元素的 k 次幂为 0。	非交换环，通常用于研究代数的奇异性质。	奇异代数结构、代数几何中的奇点。

环的整除理论 (Divisibility Theory in Rings)

虽然一般的环没有除法运算，但在某些环中，我们可以定义和研究类似于整数中的整除性质。这些环允许我们讨论因数、最大公因数、素元素等概念。常见的环中具有整除理论的例子包括：

整数环 ℤ (Integer Ring)：这是最常见的环，包含所有的整数。在这个环中，我们有完整的整除理论，例如素数、最大公因数、最小公倍数等。
欧几里得环 (Euclidean Ring)：如果一个环中可以定义一种“度量”或“大小”的概念，使得能够像在整数环中那样使用欧几里得算法来计算最大公因数，那么这个环就称为欧几里得环。例如，多项式环 𝑅[𝑥] (Polynomial Ring over Real Numbers) 和高斯整数环 ℤ[𝑖] (Gaussian Integer Ring) 都是欧几里得环。
唯一分解整环（UFD, Unique Factorization Domain）：在这些环中，元素可以唯一地分解为不可约元素的乘积，类似于整数的素数分解。比如，整数环 ℤ 和多项式环 𝑘[𝑥] (Polynomial Ring over a Field 𝑘)（其中 𝑘 是一个域）都是唯一分解整环。

域（Field）

域（Field）是一个更严格的结构，不仅加法部分形成阿贝尔群，乘法部分（不包括 0）也形成阿贝尔群，并且加法和乘法之间有分配律。

定义

一个域（Field）是一个集合（Set）和两个二元运算（Binary Operations）——加法和乘法，它满足以下条件：

加法部分：形成阿贝尔群（Additive Group）：

加法封闭性（Closure under Addition）：对于任意 a, b ∈ F，有 a + b ∈ F。
加法结合律（Associativity of Addition）：对于任意 a, b, c ∈ F，有 (a + b) + c = a + (b + c)。
加法交换律（Commutativity of Addition）：对于任意 a, b ∈ F，有 a + b = b + a。
加法单位元（Additive Identity）：存在一个元素 0 ∈ F，使得对任意 a ∈ F，有 a + 0 = 0 + a = a。
加法逆元（Additive Inverse）：对于任意 a ∈ F，存在一个元素 -a ∈ F，使得 a + (-a) = (-a) + a = 0。

乘法部分：形成阿贝尔群（不含 0 元素）（Multiplicative Group）：

乘法封闭性（Closure under Multiplication）：对于任意 a, b ∈ F，有 a ∘ b ∈ F。
乘法结合律（Associativity of Multiplication）：对于任意 a, b, c ∈ F，有 (a ∘ b) ∘ c = a ∘ (b ∘ c)。
乘法交换律（Commutativity of Multiplication）：对于任意 a, b ∈ F，有 a ∘ b = b ∘ a。
乘法单位元（Multiplicative Identity）：存在一个元素 1 ∈ F，使得对任意 a ∈ F，有 a ∘ 1 = 1 ∘ a = a。
乘法逆元（Multiplicative Inverse）：对于任意 a ≠ 0 ∈ F，存在一个元素 a⁻¹ ∈ F，使得 a ∘ a⁻¹ = a⁻¹ ∘ a = 1。

加法和乘法：分配律（Distributivity）：

对于任意 a, b, c ∈ F，有 a ∘ (b + c) = (a ∘ b) + (a ∘ c) 和 (a + b) ∘ c = (a ∘ c) + (b ∘ c)

空间（Space）

空间 (space) = 集合（set） + 结构（structure）

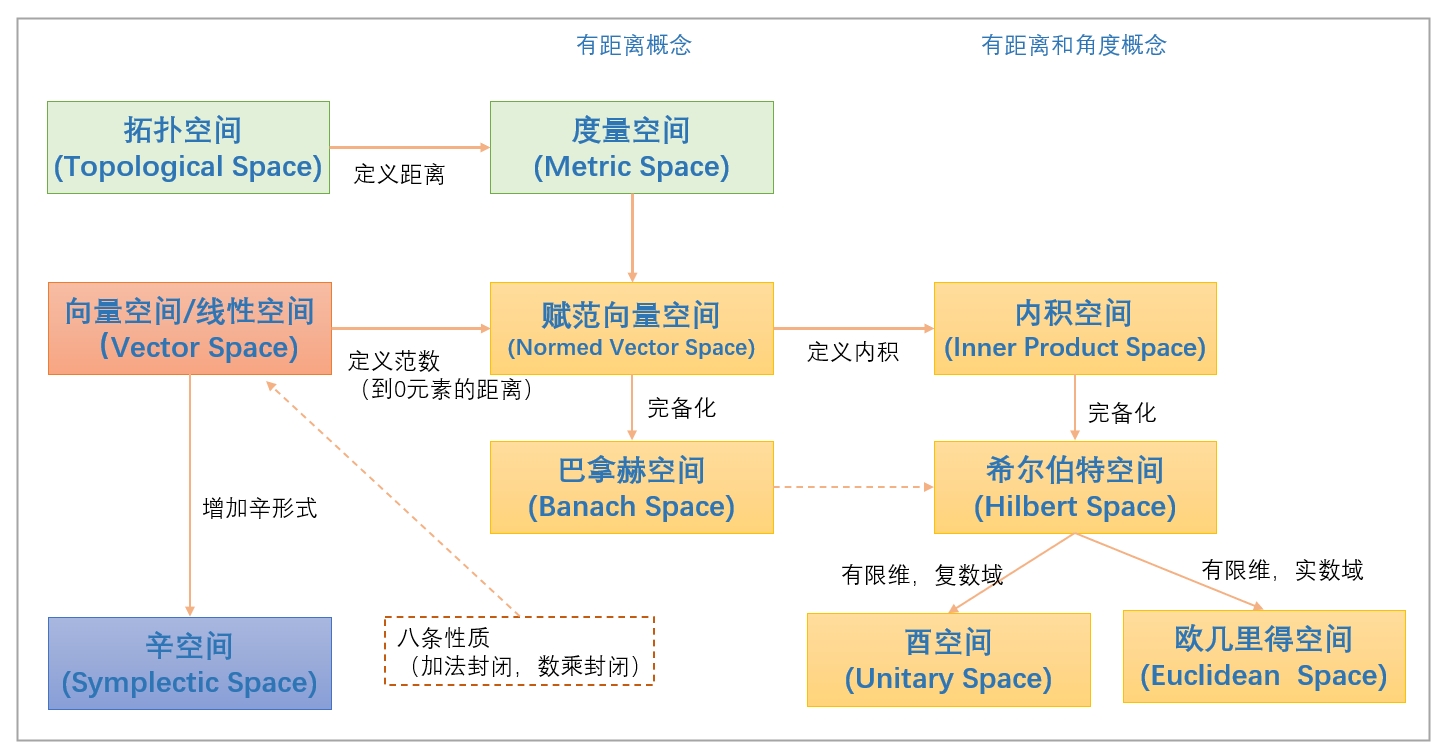
space

什么是空间？

一个空间是由一个集合以及定义在这个集合上的某种结构所组成的。根据不同的数学领域和研究的对象，结构的类型可以不同，从而产生不同类型的空间。

集合：空间的基础是一个集合。集合中的元素可以是点、向量、函数、序列、矩阵等。集合本身只是元素的一个无序集合，它没有任何额外的结构或性质。
结构：为了给集合引入更多的性质和规则，我们在集合上定义某种结构。不同的结构使得集合具备不同的几何或代数意义。

结构的种类很多，常见的包括：

拓扑结构(Topological Structure)：定义开集与闭集，研究点的邻域、收敛与连续等概念。
度量结构(Metric Structure)：定义两个点之间的距离，研究距离相关的性质，如长度、极限、连续等。
内积结构(Inner Product Structure)：定义向量之间的内积，研究角度、正交性、投影等问题。
线性结构(Linear Structure)：定义向量的加法与标量乘法，研究线性组合、线性变换等。
范数结构(Norm Structure)：定义向量的长度，研究向量的大小和收敛性等。

注意：

线性结构/向量结构是一个代数结构，研究向量的线性组合、加法和标量乘法。
拓扑结构是一个几何结构，研究集合的拓扑性质，如连续性和收敛性。

拓扑学是Topology的音译，如果意译的话，是不是会叫连续形态学，或空间结构学？？

距离，范数，内积

距离：用来度量两个点之间的“远近”。
范数：用来衡量向量的长度或大小。
内积：用来衡量两个向量之间的夹角或相似性。

它们之间的关系是：内积可以导出范数，范数可以导出距离，而内积也可以直接定义距离。

列个表：

概念	距离 (Distance)	范数 (Norm)	内积 (Inner Product)
定义	两个点之间的度量，用来衡量它们之间的“远近”。通常定义在度量空间 (Metric Space) 中。	向量的长度或大小的度量，定义在赋范向量空间 (Normed Vector Space)	两个向量之间的乘积，用来衡量它们的相似性或夹角。定义在内积空间 (Inner Product Space) 中。
主要性质	1.非负性: 𝑑(𝑥, 𝑦) ≥ 0 2. 对称性: 𝑑(𝑥, 𝑦) = 𝑑(𝑦, 𝑥) 3. 同一性: 𝑑(𝑥, 𝑦) = 0 当且仅当 𝑥 = 𝑦 4. 三角不等式: 𝑑(𝑥, 𝑧) ≤ 𝑑(𝑥, 𝑦) + 𝑑(𝑦, 𝑧)	1.非负性: ∥𝑥∥ ≥ 0 2. 齐次性: ∥𝛼𝑥∥ = \|𝛼\| ∥𝑥∥ 3. 三角不等式: ∥𝑥 + 𝑦∥ ≤ ∥𝑥∥ + ∥𝑦∥ 4. 同一性: ∥𝑥∥ = 0 当且仅当 𝑥 = 0	1.共轭对称性: ⟨𝑥, 𝑦⟩ = ⟨𝑦, 𝑥⟩̅ 2. 线性性: 对第一个变量是线性的 3. 正定性: ⟨𝑥, 𝑥⟩ ≥ 0，且 ⟨𝑥, 𝑥⟩ = 0 当且仅当 𝑥 = 0
作用	衡量点与点之间的距离，定义了空间中的几何结构。	衡量向量的长度或大小，定义了向量空间中的几何结构。	衡量两个向量之间的夹角或相似性，定义了向量空间中的角度和正交性。
与其他概念的关系	1. 距离可以从范数中导出：𝑑(𝑥, 𝑦) = ∥𝑥 − 𝑦∥（如果空间带有范数）。 2. 距离可以通过内积诱导：𝑑(𝑥, 𝑦) = √⟨𝑥 − 𝑦, 𝑥 − 𝑦⟩（如果空间带有内积）。	1. 范数可以从内积中导出：∥𝑥∥ = √⟨𝑥, 𝑥⟩（如果空间带有内积）。 2. 范数可以诱导距离：𝑑(𝑥, 𝑦) = ∥𝑥 − 𝑦∥。	1. 内积可以诱导范数：∥𝑥∥ = √⟨𝑥, 𝑥⟩ 2. 内积可以诱导距离：𝑑(𝑥, 𝑦) = √⟨𝑥 − 𝑦, 𝑥 − 𝑦⟩。
例子	欧几里得空间中的距离：𝑑(𝑥, 𝑦) = √((𝑥₁ − 𝑦₁)² + (𝑥₂ − 𝑦₂)² + … + (𝑥ₙ − 𝑦ₙ)²)。	欧几里得空间中的范数：∥𝑥∥ = √(𝑥₁² + 𝑥₂² + … + 𝑥ₙ²)。	欧几里得空间中的内积：⟨𝑥, 𝑦⟩ = 𝑥₁𝑦₁ + 𝑥₂𝑦₂ + … + 𝑥ₙ𝑦ₙ。

一些空间？

线性空间 (Vector Space)

线性空间是一个由向量组成的集合，且在该集合中定义了向量的加法和标量乘法运算。它满足加法与标量乘法的封闭性、交换律、结合律、单位元和逆元等性质。

比如：欧几里得空间 ℝⁿ 是一个线性空间。

拓扑空间 (Topological Space)

拓扑空间是一个集合 𝑋 和一组称为“开集”的子集构成的结构，满足以下条件：空集和整个集合都是开集；任意开集的并集是开集；有限个开集的交集是开集。这种结构允许我们讨论连续性、收敛性等概念。

比如：实数集 ℝ 配备标准拓扑是一个拓扑空间。

度量空间 (Metric Space)

度量空间是一个集合 𝑋，配备了一个度量（或称距离函数） 𝑑(𝑥, 𝑦)，该度量函数满足非负性、同一性、对称性和三角不等式。度量空间定义了集合中元素之间的距离。

比如：欧几里得空间 ℝⁿ 配备欧几里得度量 𝑑(𝑥, 𝑦) = √((𝑥₁ − 𝑦₁)² + … + (𝑥ₙ − 𝑦ₙ)²) 是一个度量空间。

希尔伯特空间 (Hilbert Space)

希尔伯特空间是带有内积的完备向量空间，其中内积定义了向量的长度和两个向量之间的夹角。完备性是指每个柯西序列在该空间中收敛。

比如：有限维欧几里得空间 ℝⁿ 是一个希尔伯特空间；常见的无穷维希尔伯特空间是 𝐿² 空间（平方可积函数空间）。

欧几里得空间 (Euclidean Space)

欧几里得空间是一个带有标准内积的有限维实向量空间，通常表示为 ℝⁿ。它是我们日常几何直觉中的空间，具有内积、范数和距离的概念。

比如：ℝ² 和 ℝ³ 是常见的欧几里得空间，用来描述平面和三维空间。

酉空间 (Unitary Space)

酉空间是带有复数内积的向量空间，通常是复数域上的希尔伯特空间。它的内积满足共轭对称性和正定性。酉空间中的变换保持内积不变。

比如：复数向量空间 ℂⁿ 配备标准复数内积是一个酉空间。

1+1=10

记记笔记，放松一下...