1+1=10

记记笔记，放松一下...

矩阵知识小记

理一理矩阵的知识。The Art of Linear Algebra 对线性代数的知识做了很多很直观的图表，本文中图片全部基于它们（有修改）。

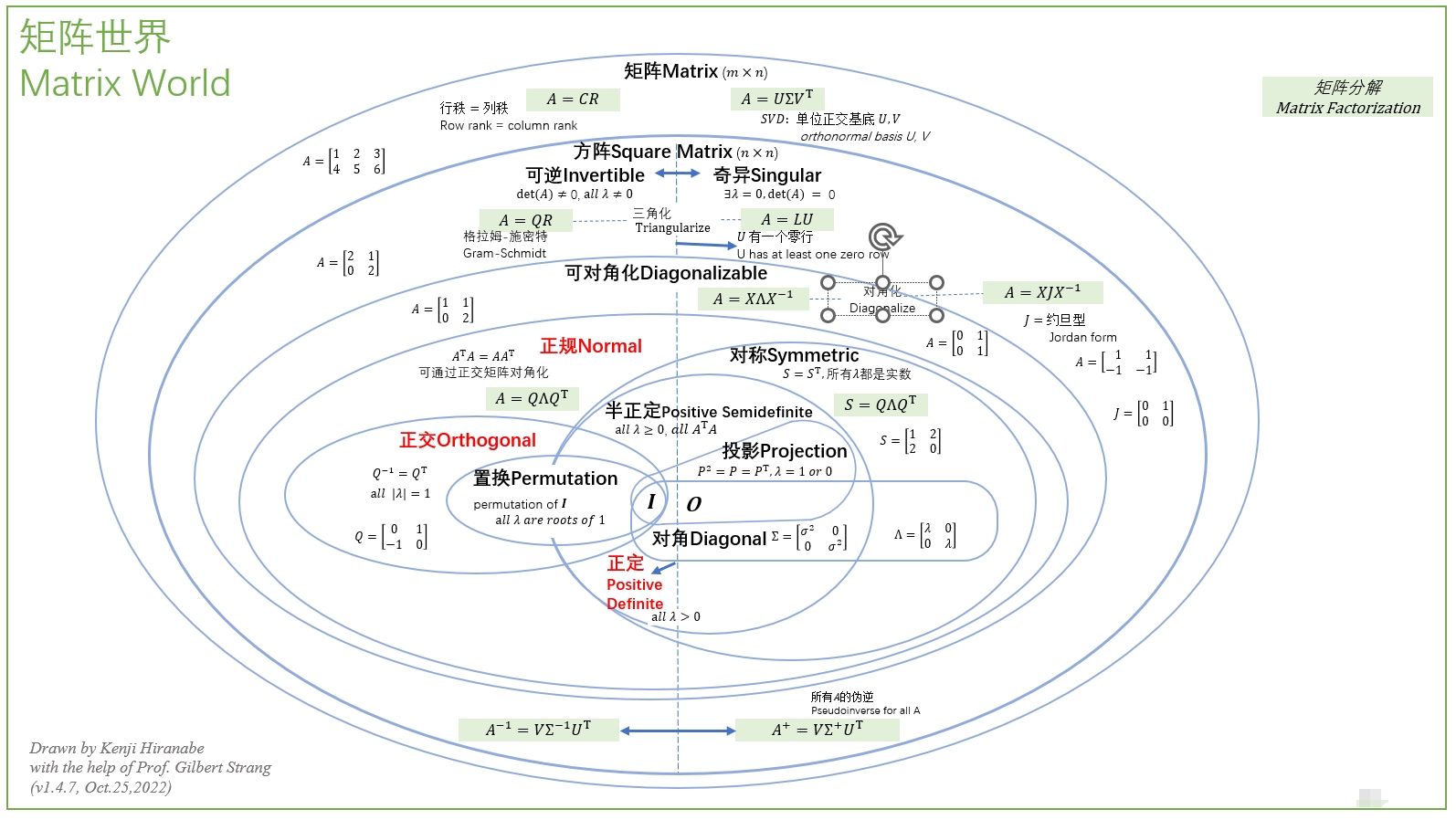
matrix world

矩阵类型

矩阵有很多类别：对称矩阵、正交矩阵、奇异矩阵、可逆矩阵、方形矩阵、可对角矩阵等等。

类别 描述 英文注解
矩阵 (Matrix) 所有矩阵A \in \mathbb{R}^{m \times n} 均可进行 QR 分解或 SVD 分解。 MatricesA \in \mathbb{R}^{m \times n} can be decomposed using QR or SVD.
方阵 (Square Matrix) 方阵A \in \mathbb{R}^{n \times n} 包括可逆矩阵或奇异矩阵。 Square matricesA \in \mathbb{R}^{n \times n} can be invertible or singular.
可逆矩阵 (Invertible Matrix) 可逆矩阵A^{-1} 存在，当且仅当 \det(A) \neq 0。 An invertible matrixA^{-1} exists if and only if \det(A) \neq 0.
奇异矩阵 (Singular Matrix) 奇异矩阵A^{-1} 不存在，且 \det(A) = 0。 A singular matrixA^{-1} does not exist, and \det(A) = 0.
可对角化矩阵 (Diagonalizable Matrix) 如果方阵A 有 n 个线性无关的特征向量，则它是可对角化的，可以表示为 A = X \Lambda X^{-1}。 If a square matrixA has n linearly independent eigenvectors, it is diagonalizable and can be written as A = X \Lambda X^{-1}.
正规矩阵 (Normal Matrix) 满足A^T A = A A^T，可以通过正交矩阵对角化为 A = Q \Lambda Q^{-1}。 SatisfiesA^T A = A A^T, and can be diagonalized by an orthogonal matrix as A = Q \Lambda Q^{-1}.
对称矩阵 (Symmetric Matrix) 对称矩阵A = A^T 是正规矩阵的子集，特征值为实数。 A symmetric matrixA = A^T is a subset of normal matrices, with real eigenvalues.
正定矩阵 (Positive Definite Matrix) 正定矩阵的所有特征值\lambda > 0。 The eigenvalues of a positive definite matrix satisfy\lambda > 0.
正半定矩阵 (Positive Semi-Definite Matrix) 正半定矩阵的所有特征值\lambda \geq 0。 The eigenvalues of a positive semi-definite matrix satisfy\lambda \geq 0.
投影矩阵 (Projection Matrix) 投影矩阵P 满足 P^2 = P = P^T，特征值为 0 或 1。 A projection matrixP satisfies P^2 = P = P^T, and its eigenvalues are 0 or 1.
正交矩阵 (Orthogonal Matrix) 正交矩阵A^{-1} = A^T，特征值的模长为 1。 An orthogonal matrix satisfiesA^{-1} = A^T, with eigenvalues of modulus 1.
置换矩阵 (Permutation Matrix) 置换矩阵P是正交矩阵的子集，是通过重新排列单位矩阵的行或列生成的，且满足 P^{-1} = P^T。 A permutation matrixP is generated by rearranging the rows or columns of the identity matrix, and satisfies P^{-1} = P^T.
反射矩阵 (Reflection Matrix) 反射矩阵是正交矩阵的一个子集，特征值为1 或 -1。 A reflection matrix is a subset of orthogonal matrices, with eigenvalues of1 or -1.
伪逆矩阵 (Pseudo-Inverse Matrix) 伪逆矩阵A^+ 可以通过奇异值分解表示为 A^+ = V \Sigma^+ U^T，即使 A 不是可逆矩阵。 The pseudo-inverseA^+ can be represented via singular value decomposition as A^+ = V \Sigma^+ U^T, even if A is not invertible.

复数域

矩阵类型 复数域上的矩阵 实数域上的对应矩阵 描述
厄米矩阵 (Hermitian Matrix) 厄米矩阵 A = A^\dagger 对称矩阵 A = A^T 复数域中，矩阵的共轭转置等于自身；实数域中，转置等于自身。
酉矩阵 (Unitary Matrix) 酉矩阵 U^\dagger U = U U^\dagger = I 正交矩阵 O^T O = O O^T = I 复数域中保持内积，实数域中保持正交性。
正定矩阵 (Positive Definite Matrix) 正定厄米矩阵 z^* A z > 0 正定对称矩阵 x^T A x > 0 复数域对复向量的二次型为正，实数域对实向量的二次型为正。
反厄米矩阵 (Skew-Hermitian Matrix) 反厄米矩阵 A^\dagger = -A 反对称矩阵 A^T = -A 复数域中，矩阵的共轭转置为负；实数域中，转置为负。
幺模矩阵 (Unimodular Matrix) 幺模矩阵 det(A) = 1 幺模矩阵 det(A) = 1 行列式绝对值为 1，复数域允许复数行列式，实数域行列式为 1 或 -1。

特征值

特征值（Eigenvalue）是一个与线性变换密切相关的重要概念。给定一个方阵 A \in \mathbb{R}^{n \times n}，特征值描述了矩阵作用在某些特殊向量（即特征向量）上时，仅改变这些向量长度而不改变方向的情况。

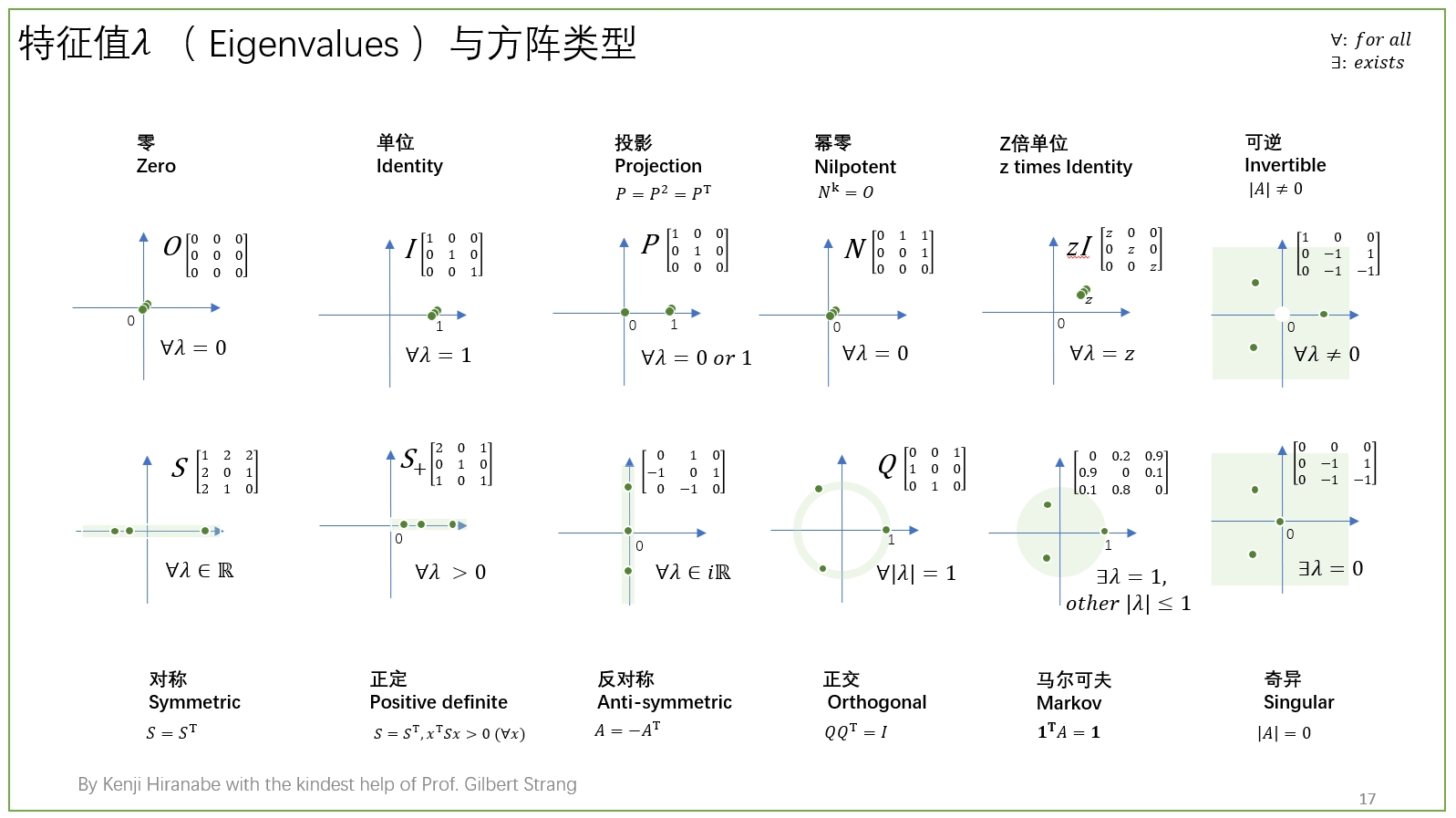
eigenvalues

特征值的定义

对于一个方阵 A，如果存在一个非零向量 v \in \mathbb{R}^n 和一个标量 \lambda，使得：

A v = \lambda v

那么 \lambda 就被称为矩阵 A 的特征值，而 v 被称为与特征值 \lambda 对应的特征向量。

几何意义

特征值在矩阵的几何变换中的物理意义。

考虑一个矩阵 A 作用在空间中的向量 v 上：

  • 如果 \lambda > 1，说明矩阵 A 对向量 v 进行了拉伸。
  • 如果 0 < \lambda < 1，则矩阵 A 对向量 v 进行了压缩。
  • 如果 \lambda = 1，向量 v 在矩阵 A 作用下保持不变。
  • 如果 \lambda = -1，则矩阵 A 将向量 v 的方向反转。
  • 如果 \lambda = 0，则矩阵 A 将向量 v 压缩为零向量。

特征值性质

  • 数量：一个 n \times n 的方阵 A 通常有 n 个特征值（包括复数特征值和重数）。
  • 重数：
    • 代数重数：特征值在特征多项式中作为根的重数。
    • 几何重数：与特征值对应的线性无关特征向量的数量，即特征空间的维数。
  • 迹和行列式：
    • 一个矩阵的迹是其所有特征值之和，即 \text{tr}(A) = \sum_{i=1}^{n} \lambda_i。
    • 一个矩阵的行列式是其所有特征值的乘积，即 \det(A) = \prod_{i=1}^{n} \lambda_i。

矩阵分解

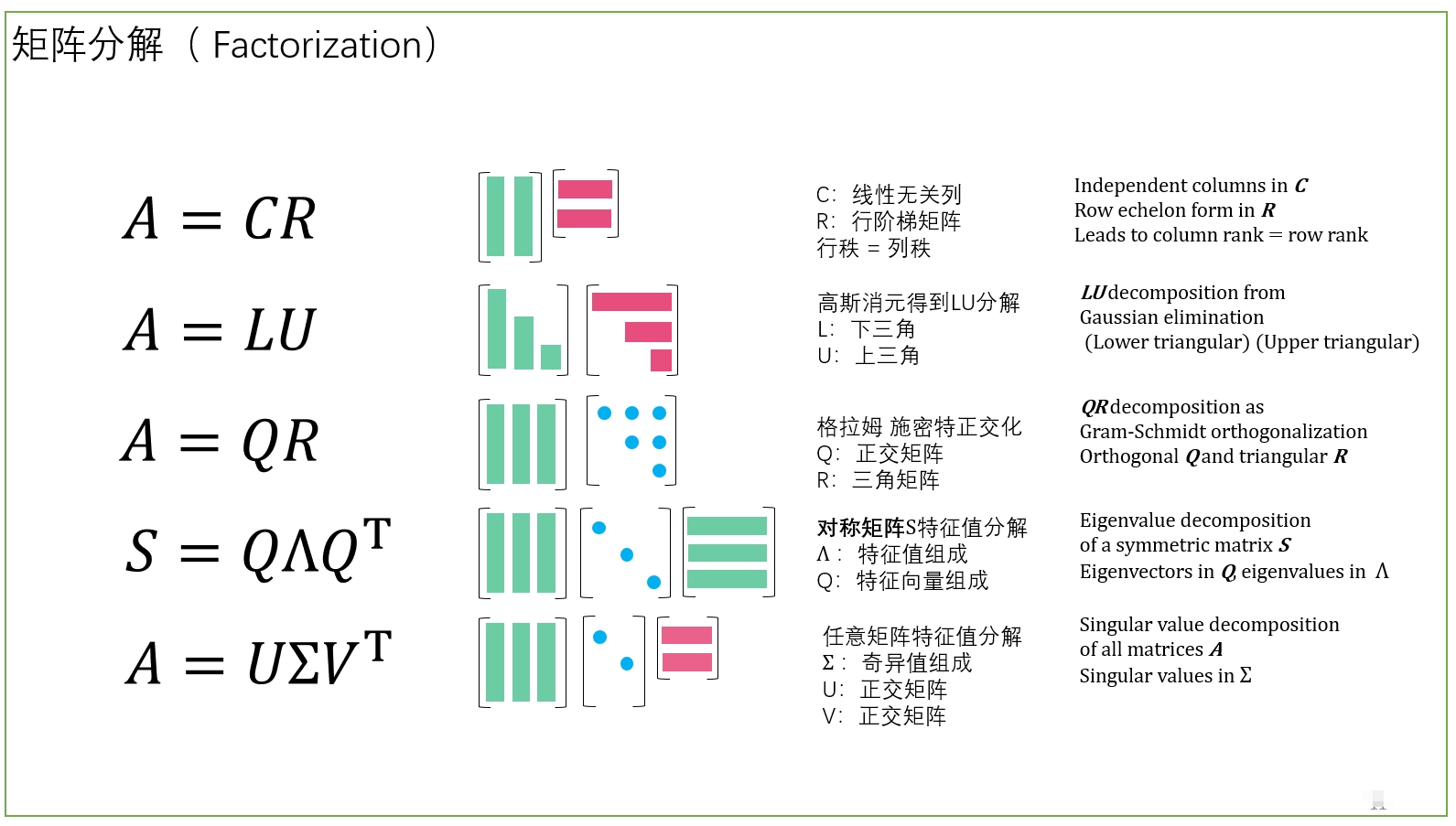
factorization

好端端的矩阵为什么要分解？？

求解线性方程组

对于线性方程组 Ax = b，直接使用矩阵 A 的逆矩阵 A^{-1} 来求解，即 x = A^{-1}b，就可以了。但为什么在实际应用中，直接用矩阵的逆来解方程并不常见？？

原因：

  1. 计算复杂度高：直接求逆矩阵的计算复杂度较高，尤其对于大规模矩阵，求逆操作的计算开销可能非常大。
  2. 数值不稳定性：求逆操作容易引入数值误差，尤其是当矩阵接近奇异时，逆矩阵的数值误差会非常明显。
  3. 效率低：相比于 LU 分解、QR 分解或 Cholesky 分解，直接求逆非常低效。通过分解矩阵，可利用三角矩阵的快速求解方法。

LU分解

LU 分解将矩阵 A 分解为下三角矩阵 L 和上三角矩阵 U，即 A = LU。这样可以将原方程 Ax = b 转化为两个更容易求解的三角方程：

A x = b \quad \Rightarrow \quad LU x = b

优点：

  • 下三角和上三角矩阵的方程组可以通过前代和回代方法快速求解
  • 如果需要针对不同的右边向量 b 求解多个方程组 Ax = b，只需要对矩阵 A 做一次 LU 分解

QR分解

QR 分解将矩阵 A 分解为正交矩阵 Q 和上三角矩阵 R，即 A = QR。这样可以将原方程 Ax = b 转化为：

Ax = b \quad \Rightarrow \quad QRx = b

通过乘以 Q^T，将方程变为 Rx = Q^T b，即：

QR x = b \quad \Rightarrow \quad R x = Q^T b

由于 R 是上三角矩阵，使用回代法可以快速求解 x。

优点：

  • 稳定性高：QR 分解在数值计算中比 LU 分解更稳定，尤其在处理病态矩阵（即条件数很大的矩阵）时，它能够更好地避免误差的积累。
  • 最小二乘法：QR 分解特别适合用于求解过定方程组（即方程的数量多于未知数的情况），这种情况下可以通过最小二乘法来求解，而 QR 分解是最常用的最小二乘法工具之一。

降维与压缩

在数据降维和压缩领域。通过矩阵分解技术，可以有效地减少数据的维度或存储空间，同时保留大部分信息。

奇异值分解 (SVD)：

SVD 将矩阵 A \in \mathbb{R}^{m \times n} 分解为三个矩阵的乘积：

A = U \Sigma V^T

其中：

  • U 是 m \times m 的正交矩阵，表示左奇异向量。
  • \Sigma 是 m \times n 的对角矩阵，包含矩阵的奇异值（按大小排序）。
  • V^T 是 n \times n 的正交矩阵，表示右奇异向量。

通过 SVD 分解矩阵，奇异值矩阵 \Sigma 的对角元素（奇异值）按大小递减排列。较大的奇异值对应了数据中的重要信息，而较小的奇异值对应了噪声或冗余信息。通过截断较小的奇异值，可以减少矩阵的维度，但保留大部分原始数据的结构。

如果只保留前 k 个最大的奇异值和对应的奇异向量，得到的矩阵 A_k 是原矩阵的低秩近似（降维）：

A_k = U_k \Sigma_k V_k^T

其中 U_k 和 V_k 只保留前 k 列，\Sigma_k 是前 k 个奇异值构成的对角矩阵。

矩阵

Matrix 中文翻译成矩阵，日文翻译为行列（ぎょうれつ，gyōretsu），而 Determinant 在中文和日文中都是行列式。

Vector 在中文中翻译比较乱：

  • 数学：向量。向 表示方向；量 表示大小和数量
  • 物理：矢量。矢 表示箭头，暗示方向；量 表示大小和数量。
  • C++：动态数组

矩阵定义

一个 m \times n 的矩阵 A 是一个包含 m 行 n 列的二维数组，可以表示为：

A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}

其中，a_{ij} 表示矩阵 A 的第 i 行、第 j 列的元素。A 的维度或大小为 m \times n。

向量定义

向量可用列向量或行向量。但是 列向量更为常见：

\mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix}

列向量相对于行向量的好处：

  • 线性代数的标准惯例：列向量是线性代数中的标准表示法，符合大多数教材和学术文献的习惯。
  • 矩阵运算的兼容性：在矩阵乘法中，矩阵通常是左乘列向量的，这使得矩阵运算更方便和直观。
  • 线性变换的表示：线性变换通常用矩阵作用在列向量上，列向量更符合这种变换的顺序。
  • 向量空间的表示：向量空间的基向量通常按列排列，列向量有助于更清晰地表达向量的线性组合。

视角！！

The Art of Linear Algebra 很大篇幅在以不同视角可视化矩阵的运算。

1个 (mxn) 的矩阵，可以视为：

  • 1个矩阵
  • mn个数
  • n个列
  • m个行

1个向量通常用列向量表示，行向量可以用列向量的转置表示。

对于乘法，可以结合多视角看待：

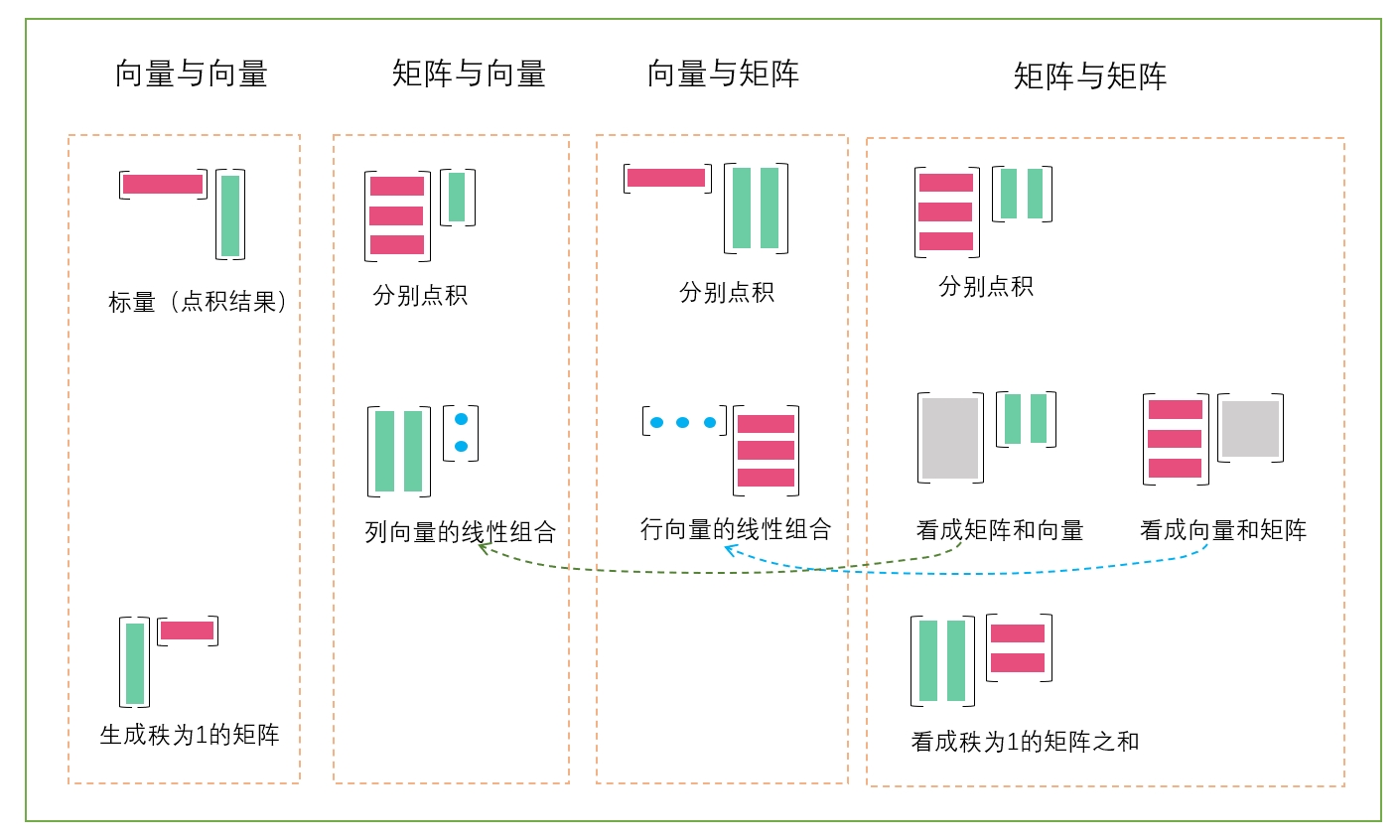
matrix_multiplication

基本运算

  • 矩阵加法 (Matrix Addition)：两个相同大小矩阵的元素对应相加。
  • 矩阵乘法 (Matrix Multiplication)：两个矩阵相乘，按行列对应的内积计算。
  • 标量乘法 (Scalar Multiplication)：矩阵的每个元素乘以一个标量。
  • 矩阵转置 (Matrix Transposition)：将矩阵的行和列互换。
  • 矩阵的逆 (Matrix Inversion)：对于可逆矩阵 A，找到 A^{-1}，使得 A \times A^{-1} = I。
  • 迹 (Trace)：方阵主对角线元素的和。
  • 行列式 (Determinant)：方阵的一个标量值，用于判断矩阵是否可逆。【行列式是一个值】

复数域矩阵

在复数域，矩阵有如下运算：

  • 共轭操作（Conjugation）:将每个元素替换为其复共轭。
  • 共轭转置（Conjugate Transpose / Hermitian Transpose）：先对矩阵进行转置，然后对每个元素取复共轭
操作 复数域 实数域
复共轭 (Conjugation) 对矩阵元素取复数共轭 \overline{A} 无此操作
共轭转置 (Conjugate Transpose) 共轭转置 A^\dagger = (\overline{A})^T 退化为普通转置 A^T
特征值和特征向量 (Eigenvalues and Eigenvectors) 允许复数特征值和复数特征向量 特征值可能是复数，但特征向量是实数的线性组合
对角化 (Diagonalization) 所有矩阵都可以在复数域上对角化或化成约当标准形 不是所有矩阵都可对角化
旋转和相位 (Rotation and Phase) 支持复数相位旋转 e^{i\theta} 仅支持实数旋转

参考

  • https://github.com/kenjihiranabe/The-Art-of-Linear-Algebra
  • https://en.wikipedia.org/wiki/Matrix_(mathematics)
  • https://github.com/Visualize-ML/Book4_Power-of-Matrix

Posted by Debao Zhang Science