1+1=10

记记笔记，放松一下...

傅里叶变换小记

东南大学《工程数学·积分变换》主要介绍傅里叶变换和拉普拉斯变换；顾樵《数学物理方法》二三四章都在介绍这两个变换；ALAN V. OPPENHEIM《信号与系统》二三四九十章都在介绍积分变换；《数字图像处理》...

傅里叶认为，任何复杂的周期信号都可以用一组简单的正弦波（sine waves，即不同频率的正弦和余弦函数）表示。这种方法不仅适用于光滑的信号，也适用于不光滑的信号（例如锯齿波，sawtooth wave），甚至是 不连续 的信号（discontinuous signals）。

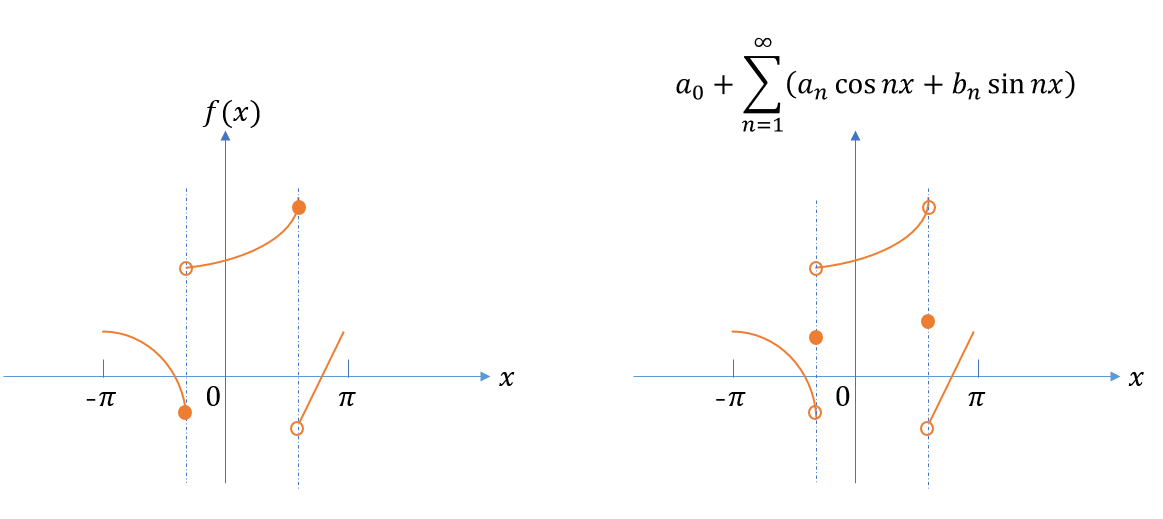
fourier series

这就是现在所说的 傅里叶级数。后来，这一思想被推广到更广泛的领域，包括 傅里叶变换 和 离散傅里叶变换。

img

学术争议

傅里叶提出的用正弦和余弦函数表示任意周期函数的观点，实际上是引入了 正交基（orthogonal basis）的概念。今天我们知道，正弦和余弦函数组成了一个 完备的函数集（complete function set），可以用于表示任何周期函数。然而，在傅里叶所处的时代，这一想法是前所未有的，并不为大多数数学家所接受。

困境

由于当时 数学分析（mathematical analysis），特别是关于 函数收敛性（convergence of functions）的理论还处于发展的早期阶段，傅里叶的工作缺乏严格的数学基础。他并没有明确给出傅里叶级数（Fourier series）的收敛条件，或证明这些级数在一定条件下会收敛到原函数。

在傅里叶之前的10多年，著名数学家 欧拉（Leonhard Euler）和 伯努利（Daniel Bernoulli）在研究弦振动（vibrating strings）时也提出过类似的 正弦波叠加（superposition of sine waves）的想法，但他们并没有深入研究这一概念。事实上，欧拉本人后来放弃了使用 三角函数级数（trigonometric series）来表示函数的想法。

争议

在傅里叶的同代人中，著名数学家 约瑟夫·拉格朗日（Joseph-Louis Lagrange）和 西蒙·泊松（Siméon Denis Poisson）是傅里叶理论的强烈反对者。

  • 拉格朗日：拉格朗日质疑傅里叶级数的 严谨性（rigor）。他认为傅里叶声称的“任意函数”可以分解为正弦和余弦函数的和，这一观点过于宽泛。拉格朗日坚持认为，只有非常光滑且具有 连续一阶导数（continuously differentiable functions）的函数才能用这种方法表示出来。他尤其怀疑傅里叶级数是否能适用于 不连续函数（discontinuous functions）。
  • 泊松：泊松则从物理角度质疑傅里叶的观点，认为傅里叶的数学方法可能与物理现实不符。他特别关注傅里叶级数在处理 边界条件（boundary conditions）时的有效性问题，并认为傅里叶的理论在物理应用中可能并不适用。

发展

  • 狄利克雷（Johann Peter Gustav Lejeune Dirichlet）为傅里叶级数的 收敛性（convergence）问题提供了严格的数学证明，定义了 狄利克雷条件（Dirichlet conditions），从而解决了拉格朗日和泊松等人关于傅里叶级数收敛性的担忧。
  • 奥古斯丁·柯西（Augustin Cauchy）和 皮埃尔·西蒙·拉普拉斯（Pierre-Simon Laplace）等人也对傅里叶的理论表示支持，并对其进行了进一步的完善，推动了傅里叶级数和傅里叶变换在数学和物理中的应用。

傅里叶级数 到 傅里叶变换

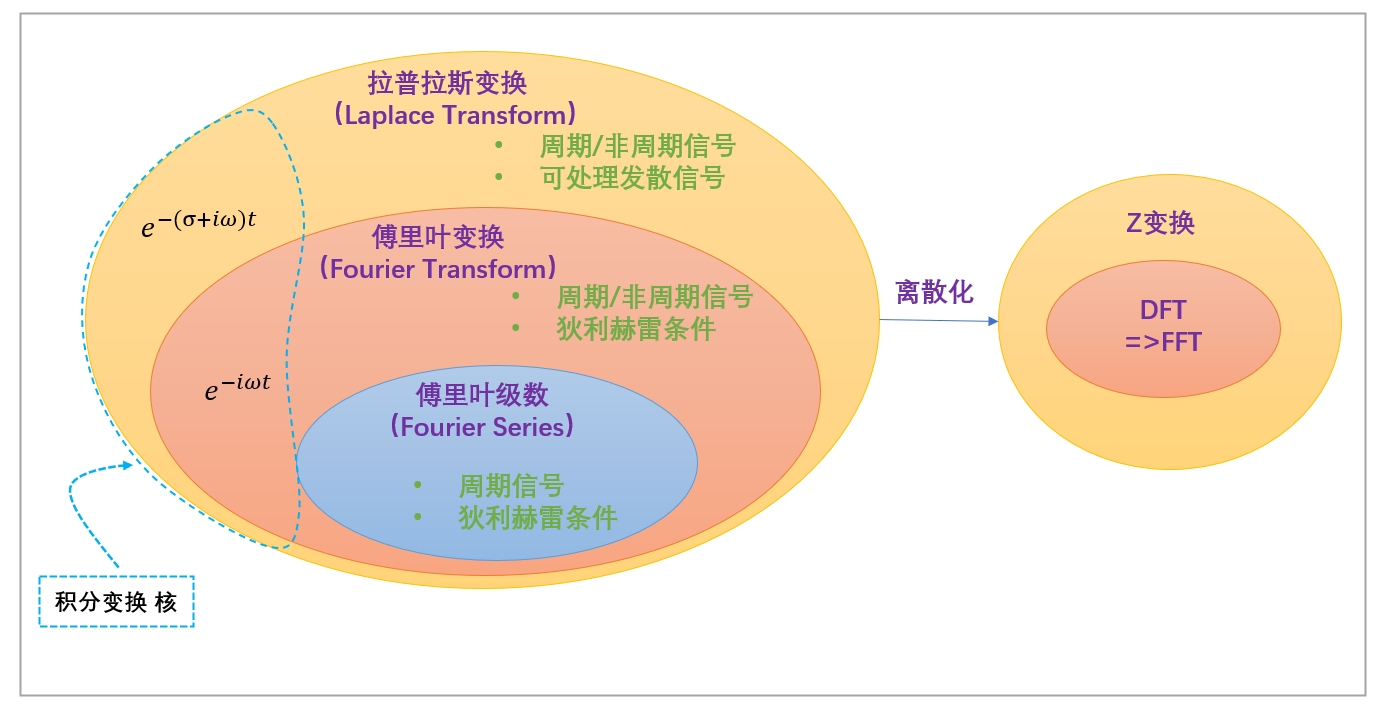
傅里叶级数 和 傅里叶变换 是傅里叶分析的核心工具。傅里叶积分则是傅里叶变换的中间形式。

  • 傅里叶级数（Fourier Series）：用于表示周期信号的离散频谱（discrete spectrum of periodic signals）。
  • 傅里叶积分（Fourier Integral）：用于处理非周期信号的连续频谱（continuous spectrum of non-periodic signals）。
  • 傅里叶变换（Fourier Transform）：最广泛的形式，用于任意信号的时域到频域转换。
对比项 傅里叶级数（Fourier Series） 傅里叶积分（Fourier Integral） 傅里叶变换（Fourier Transform）
适用对象 周期信号（periodic signals） 非周期信号（aperiodic signals） 任意信号（any signals）
频谱 离散频谱（discrete spectrum） 连续频谱（continuous spectrum） 连续频谱（continuous spectrum）
展开方式 离散频率下的正弦和余弦函数的和 频率连续变化的正弦和余弦函数的积分 频率连续变化的正弦和余弦函数的积分
应用领域 处理周期性现象，如振动、波动等 对非周期信号的频率分析 广泛

傅里叶级数

对于周期为 T 的函数 f(t) ，它可以展开为傅里叶级数：

f(t) = \frac{a_0}{2} + \sum_{n=1}^{\infty} \left( a_n \cos\left( \frac{2\pi n t}{T} \right) + b_n \sin\left( \frac{2\pi n t}{T} \right) \right)

其中，傅里叶系数 a_n 和 b_n 通过以下公式计算：

a_n = \frac{2}{T} \int_{0}^{T} f(t) \cos\left( \frac{2\pi n t}{T} \right) dt \\ b_n = \frac{2}{T} \int_{0}^{T} f(t) \sin\left( \frac{2\pi n t}{T} \right) dt

在傅里叶级数中，周期函数的频率是离散的，正弦波的频率是其周期的整数倍。然而，在处理非周期信号（aperiodic signals）时，傅里叶级数不再适用，因为此时频率将不再是离散的，而是连续的。

正交基（Orthogonal Basis）

泰勒级数的基底函数：1, x^2, x^3, x^4, ...

傅里叶级数的基底函数：1, \cos x, \cos 2x, \cos 3x, ..., \sin x, \sin 2x, \sin 3x, ...

与泰勒级数不同，傅里叶级数的任意两个基底函数，在区间 [0, 2\pi]上都是正交的。

狄利赫雷定理（Dirichlet's Theorem）

傅里叶级数用于将周期函数表示为正弦和余弦函数的无穷级数，狄利赫雷定理给出了傅里叶级数收敛的条件。

如果一个周期为 T 的函数 f(x) 满足以下条件，则它的傅里叶级数在每个点都收敛于 f(x) 在该点的值（或者在不连续点处收敛于左右极限的平均值）：

  1. 周期性（Periodicity）：f(x) 是一个周期为 T 的周期函数。
  2. 分段连续（Piecewise Continuity）：函数 f(x) 在一个周期内至多有有限个不连续点，并且在这些不连续点处的左极限和右极限存在。
  3. 分段光滑（Piecewise Smoothness）：函数 f(x) 在一个周期内至多有有限个极值点，并且在这些点之间，函数是可微的，且导数连续。

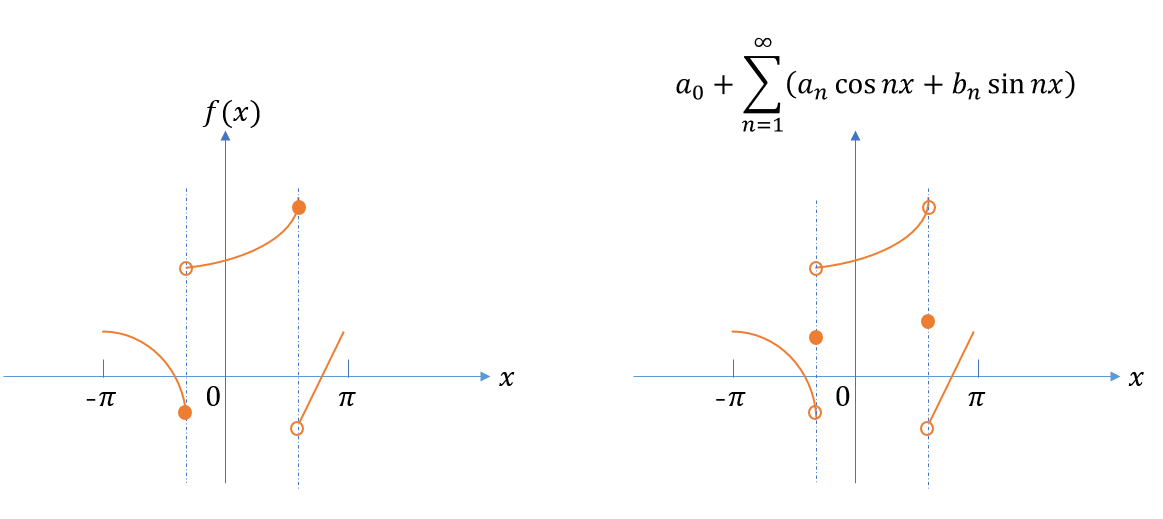
fourier series

意味着：

  • 在连续点上：傅里叶级数收敛于函数 f(x) 的值。
  • 在不连续点上：傅里叶级数收敛于该点的左右极限的平均值，即：
\text{傅里叶级数在不连续点} \ x_0 \ \text{上收敛于} \ \frac{f(x_0^-) + f(x_0^+)}{2}

傅里叶积分

傅里叶积分是连接傅里叶级数和傅里叶变换的桥梁，它适用于 非周期函数（non-periodic function）。当周期趋于无穷大时，傅里叶级数过渡为傅里叶积分。

对于非周期函数 f(t) ，我们可以使用傅里叶积分来表示（不使用复数时，注意积分范围[0, \infty)）：

f(t) = \int_{0}^{\infty}[A(\omega)\cos\omega t+B(\omega)\sin\omega t]d\omega

其中，傅里叶系数 A(\omega) 和 B(\omega) 通过以下公式计算：

A(\omega) = \frac{1}{\pi} \int_{-\infty}^{\infty} f(t) \cos\omega t dt \\ B(\omega) = \frac{1}{\pi} \int_{-\infty}^{\infty} f(t) \sin\omega t dt

当使用复数表达时，上下限就变成(-\infty, \infty)

f(t) = \int_{-\infty}^{+\infty} F(\omega) e^{-j\omega t } \mathrm{d} \omega

其中：

F(\omega) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}f(\tau)e^{-j\omega\tau} \mathrm{d}\tau

傅里叶积分定理

傅里叶积分的前提是：f(t) 在 (-\infty, +\infty) 上满足如下条件：

  • f(t) 在任一有限区间满足 狄利赫雷条件。
  • f(t) 在无限区域上绝对可积！！

那么，什么是...

绝对可积（absolutely integrable）

从傅里叶级数到傅里叶积分转变过程中，绝对可积是一个重要概念。

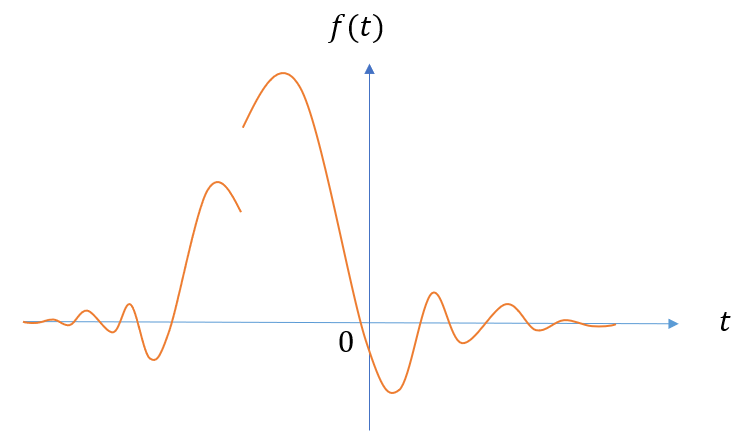
absolutely_integrable

如果f(t)在 (-\infty, +\infty) 上满足如下条件：

\int_{-\infty}^{\infty} \lvert f(t) \rvert \mathrm{d}t < \infty

则称为 f(t) 绝对可积。

该条件可以确保前面 A(\omega) 和 B(\omega) 对 f(t) 乘以绝对值小于1的三角函数后一定时可积分的。

傅里叶变换

对于定义在实数轴上 t \in (-\infty, \infty) 的函数 f(t) ，傅里叶变换定义为：

F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i \omega t} dt

这里， F(\omega) 是信号 f(t) 在频率 \omega 上的傅里叶变换，表示信号的频谱。

逆傅里叶变换 可以将频域的函数转换回时域，其定义为：

f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) e^{i \omega t} d\omega

可以看出，f{t} 和 F(\omega) 可以互相表达。其中

傅里叶变换式 可以记为：

F(\omega) = \mathcal{F}[f(t)]

傅里叶逆变换式记为：

f(t) = \mathcal{F}^{-1}[F(\omega)]

周转圆（Epicycle）

1
2
    Epicycle(frequency=1, amplitude=3, phase=0),
    Epicycle(frequency=-3, amplitude=1, phase=0),

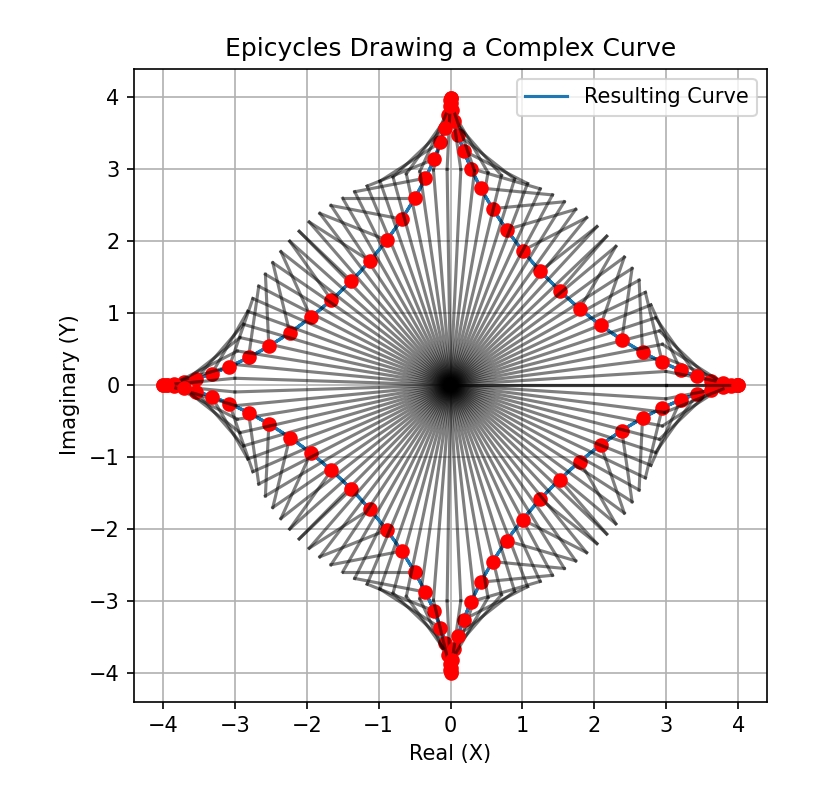
epicycles

Epicycle（周转圆）是古代天文学家用来解释天体运动的几何模型，特别是为了描述行星的复杂轨迹。这个概念最早由托勒密（Ptolemy）提出，主要用于解释在地心模型中看到的行星逆行现象。

在周转圆模型中，行星并不直接绕地球运动，而是首先围绕一个小圆（周转圆）运动，而这个小圆的中心则绕着一个大圆（称为本轮，deferent）运动。通过这种双重旋转，古代天文学家能够近似描述行星的复杂轨迹。

傅里叶级数和傅里叶变换是将函数分解为多个频率的正弦波或复数指数函数的叠加。这些正弦波可以看作是不同频率的"周转圆"。 在傅里叶级数中，每个离散频率的复数指数函数对应一个"周转圆"，而傅里叶变换中每个连续频率的复数指数函数也可以看作一个"周转圆"。

花体符号表示

傅里叶变换 通常用 花体的 \mathcal{F} 表示：

\mathcal{F}\{f(t)\} = F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i \omega t} dt

其中，\mathcal{F} 表示傅里叶变换运算符，将时域中的信号 f(t) 转换为频域中的信号 F(\omega)。

与此类似，后面提到的拉普拉斯变换通常用 花体的 \mathcal{L} 表示：

\mathcal{L}\{f(t)\} = F(s)

其中，\mathcal{L} 表示拉普拉斯变换运算符，将时域信号 f(t) 转换为复频域中的信号 F(s)。

离散傅里叶变换（DFT）

离散傅里叶变换（DFT） 的思想源自傅里叶的工作，但它的真正发展得益于 20 世纪中期计算机和数字信号处理的进步。特别是在 J. W. Cooley 和 John Tukey 在 1965 年提出的 快速傅里叶变换（FFT）算法后。

对于长度为 N 的序列 x[n]，它的离散傅里叶变换 X[k] 定义为：

X[k] = \sum_{n=0}^{N-1} x[n] e^{-i \frac{2\pi}{N} kn}, \quad k = 0, 1, \dots, N-1

其中：

  • x[n] 是时域的离散信号，
  • X[k] 是频域的离散傅里叶系数，
  • N 是信号的长度，
  • i 是虚数单位。

逆离散傅里叶变换（Inverse Discrete Fourier Transform, IDFT）的定义为：

x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] e^{i \frac{2\pi}{N} kn}, \quad n = 0, 1, \dots, N-1

通过 DFT，我们可以将时域的离散信号 x[n] 转换为频域信号 X[k]，而通过 IDFT，可以将频域信号 X[k] 转换回时域信号 x[n]。

FFT（Fast Fourier Transform）

FFT（Fast Fourier Transform）是快速计算 DFT（Discrete Fourier Transform）的高效算法，将复杂度从 O(N^2) 降低到 O(N \log N)。它通过分治法（divide and conquer）将大规模问题分解为多个小规模问题，再递归求解。

FFT的分治思想依赖于蝴蝶操作（Butterfly Operation），它通过反复将DFT分解为两个规模分别为 N/2 的DFT。具体来说，FFT利用了偶数项和奇数项的分解：

X[k] = \sum_{n=0}^{N-1} x[n] e^{-i \frac{2\pi}{N} kn}

可以拆分为：

X[k] = \sum_{n=0}^{N/2 - 1} \left( x[2n] e^{-i \frac{2\pi}{N} k(2n)} + x[2n+1] e^{-i \frac{2\pi}{N} k(2n+1)} \right)

通过这种方法，FFT算法将问题的规模从 N 逐步减少到 N/2、N/4，直到可以直接求解最小规模的DFT。

注意：

  • 信号长度：经典的Cooley-Tukey FFT算法通常要求输入信号长度为2的幂次方。对于不满足这一条件的信号，通常需要进行零填充（padding）来扩展信号长度。
  • 窗口效应：FFT假设信号是周期性的，对于非周期信号，直接使用FFT可能会引入伪频谱（leakage）问题。为此，通常会使用窗函数（window function）来减少这种效应。

傅里叶变换 到 拉普拉斯变换（Laplace Transform）

傅里叶变换有广泛应用，但也有明显的局限性...

傅里叶变换局限性

傅里叶变换要求函数在负无穷到正无穷的整个区间上都有定义，并且满足一定的条件，才能保证傅里叶变换的存在和收敛。

  • 1 函数在整个实数轴上定义： 对于一个信号或函数 f(t)，其傅里叶变换的定义是基于从 -\infty 到 \infty 的积分：
F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i \omega t} dt

意味着 f(t) 必须在整个区间 (-\infty, \infty) 上有定义。

  • 2 绝对可积性： 傅里叶变换的一个重要条件是绝对可积性，即函数 f(t) 的绝对值的积分在整个实数范围内必须是有限的：
\int_{-\infty}^{\infty} |f(t)| dt < \infty

这通常被称为 狄利赫雷条件（Dirichlet conditions） 之一。绝对可积性确保了傅里叶变换的收敛性，即傅里叶变换在频域中的结果（频谱）能有效地存在。

考虑

对于任意一个函数 g(t)(t\ge 0)，如何才能做傅里叶变换？

  1. 确保定义域是 (-\infty, \infty)，乘以阶跃函数u(t)：
g(t)u(t)
  1. 要保证绝对可积，再乘以衰减因子\exp (-\beta t)(\beta > 0)：
g(t)u(t)\exp(-\beta t)

这样一来，就可以进行变换了：

\int_{-\infty}^{\infty} g(t)u(t)\exp(-\beta t) e^{-i\omega t}\mathrm{d}t = \int_{0}^{\infty}f(t)e^{pt}\mathrm{d}t

其中：f(t)=g(t)u(t)，p=\beta + i\omega。

拉普拉斯变换

拉普拉斯变换（Laplace Transform）用于将一个时域信号转换为复频域信号（complex frequency domain signal，复数 s 的函数）。它比傅里叶变换更广泛，因为它可以处理不仅仅是稳定信号（stable signals），还可以处理不稳定信号（unstable signals），如指数增长的信号。对于时域信号 f(t)，拉普拉斯变换定义为：

F(s) = \int_{0}^{\infty} f(t) e^{-st} dt

其中：

  • f(t) 是时域信号（time-domain signal）。
  • F(s) 是复频域信号（complex frequency-domain signal），s 是复数，表示为 s = \sigma + i \omega，其中 \sigma 是实部，\omega 是虚部。

拉普拉斯变换的逆变换（inverse transform）为：

f(t) = \frac{1}{2\pi i} \int_{\sigma - i \infty}^{\sigma + i \infty} F(s) e^{st} ds

其中积分路径通常位于复平面（complex plane）上的某条直线。

z变换

Z 变换是离散时间的拉普拉斯变换。通过 z = e^{sT}（T 为采样周期），Z 变换可以看作离散系统的拉普拉斯变换。

对于一个离散时间信号 x[n]，其 Z 变换 定义为：

X(z) = \sum_{n=-\infty}^{\infty} x[n] z^{-n}

其中 z 是复数变量，通常表示为 z = re^{i\omega}。

逆 Z 变换用于将复频域中的信号 X(z) 转换回时域信号 x[n]，其定义为：

x[n] = \frac{1}{2\pi i} \oint_C X(z) z^{n-1} dz

其中 C 是围绕收敛区域的一条闭合路径。

z变换与离散傅里叶变换（DFT）

当 z 落在单位圆 |z| = 1 上时，Z 变换退化为离散傅里叶变换：

X(e^{i\omega}) = \sum_{n=-\infty}^{\infty} x[n] e^{-i \omega n}

因此，Z 变换是 DFT 的广义形式，可以处理更广泛的信号类型。

积分变换（Integral Transform）

傅里叶变换和拉普拉斯变换都是积分变换的一种，只是核函数不同。

积分变换是通过积分操作将一个函数从一个域（通常是时域或空间域）转换到另一个域（通常是频域或复频域）的数学工具。其定义：

F(s) = \int_{a}^{b} K(s, t) f(t) dt

其中：

  • f(t) 是待变换的函数。
  • F(s) 是变换后的函数。
  • K(s, t) 是核函数（Kernel Function），决定了变换的特性。
  • s 是变换后的变量。

对傅里叶变换公式来说，核函数是 e^{-i \omega t}（其中，\omega 是频率变量，i 是虚数单位）：

F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i \omega t} dt

对拉普拉斯变换公式来说，核函数是e^{-st}（其中，s 是复频率变量，可以写作 s = \sigma + i \omega，包含实部 \sigma 和虚部 i \omega）：

F(s) = \int_{0}^{\infty} f(t) e^{-st} dt

卷积（Convolution）

傅里叶变换与卷积关系：傅里叶变换将卷积运算转化为频域中的简单乘积运算，即两个函数的卷积在频域中对应它们傅里叶变换的乘积。

卷积在物理上描述了如何将一个输入信号（input signal）通过一个线性时不变系统（linear time-invariant system, LTI），得到输出信号（output signal）。例如，在电子电路中，输入信号通过滤波器后的输出可以用卷积来描述：

  • f(t)：输入信号（input signal）。
  • g(t)：滤波器的时域响应（impulse response）。
  • (f * g)(t)：滤波器对输入信号的输出（output of the filter）。

定义

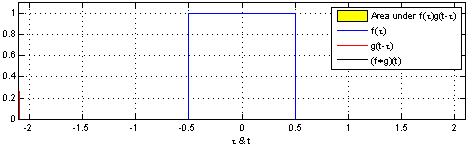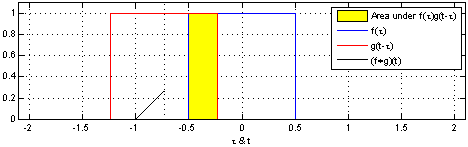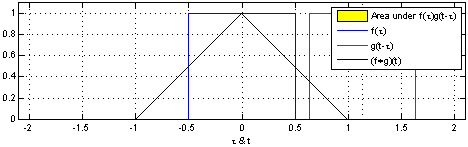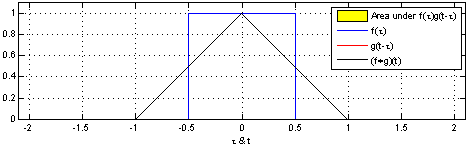
convolution

连续卷积（Continuous Convolution）

对于两个连续函数 f(t) 和 g(t)，它们的卷积 (f * g)(t) 定义为：

(f * g)(t) = \int_{-\infty}^{\infty} f(\tau) g(t - \tau) d\tau

这意味着，函数 f(t) 在时间 t 时刻的卷积结果是 g(t) 的每个时刻与 f(t) 的整体相互作用的加权和。

  • f(t)：输入信号（input signal）。
  • g(t)：系统的脉冲响应（impulse response）或滤波器（filter）。

离散卷积（Discrete Convolution）

对于离散信号 x[n] 和 h[n]，它们的卷积 (x * h)[n] 定义为：

(x * h)[n] = \sum_{k=-\infty}^{\infty} x[k] h[n - k]

卷积定理（Convolution Theorem）

卷积与傅里叶变换（Fourier Transform）的关系，主要通过卷积定理（Convolution Theorem）来体现。

卷积定理指出：

时域中的卷积 对应 频域中的乘积：

\mathcal{F}\{f(t) * g(t)\} = F(\omega) \cdot G(\omega)

即，两个时域信号的卷积，其傅里叶变换等于它们傅里叶变换的乘积。

频域中的卷积 对应 时域中的乘积：

\mathcal{F}^{-1}\{F(\omega) * G(\omega)\} = f(t) \cdot g(t)

即，两个频域信号的卷积，其逆傅里叶变换等于它们时域信号的乘积。

拉普拉斯卷积定理（Laplace Convolution Theorem）

拉普拉斯变换主要用于分析线性时不变系统（linear time-invariant systems, LTI）的响应。在这种情况下，输入信号 f(t) 和系统的单位脉冲响应 h(t) 的卷积描述了系统的输出。

时域中的卷积 对应 频域中的拉普拉斯乘积：

\mathcal{L}\{f(t) * g(t)\} = F(s) \cdot G(s)

即，两个时域信号的卷积，其拉普拉斯变换等于它们拉普拉斯变换的乘积。

频域中的拉普拉斯卷积 对应 时域中的乘积：

\mathcal{L}^{-1}\{F(s) * G(s)\} = f(t) \cdot g(t)

即，两个拉普拉斯域信号的卷积，其逆拉普拉斯变换等于它们时域信号的乘积。

参考

  • 《Signals & Systems》ALAN V. OPPENHEIM
  • 2Blue1Brown But what is the Fourier Transform? A visual introduction.
  • https://www.jezzamon.com/fourier/zh-cn.html
  • http://www.limit-point.com/blog/2023/epicycles/
  • https://en.wikipedia.org/wiki/Fourier_transform
  • https://en.wikipedia.org/wiki/Laplace_transform
  • https://en.wikipedia.org/wiki/Discrete_Fourier_transform
  • https://en.wikipedia.org/wiki/Convolution

Posted by Debao Zhang Science