只接触过大学物理,没学过量子力学,胡乱记录一些基础东西...
在量子力学,通过薛定谔方程可以来理解电子云的分布。氢原子是最简单的原子系统,只有一个质子和一个电子,薛定谔方程可以有解析解。而氦原子有两个电子,就已经超级复杂,只能用近似方法求解了。
概念
粒子的量子态是由波函数\psi(\mathbf{r}, t)来描述的。这个波函数包含了这个粒子可能有的一切信息。
薛定谔方程
薛定谔方程是量子力学的基本方程,它描述了量子系统中粒子的波动行为。其一般形式为:
i\hbar \frac{\partial}{\partial t} \psi(\mathbf{r}, t) = \hat{H} \psi(\mathbf{r}, t)
其中:
- i 是虚数单位,
- \hbar 是约化普朗克常数,
- \frac{\partial}{\partial t} 是对时间的偏导数,
- \psi(\mathbf{r}, t) 是波函数,依赖于位置 \mathbf{r} 和时间 t,
- \hat{H} 是哈密顿算符,它描述了系统的总能量(包括动能和势能)。
对于一个质量为m的粒子在势场 V(\mathbf{r}, t) 中运动的情况,哈密顿算符通常可以表示为:
\hat{H} = -\frac{\hbar^2}{2m} \nabla^2 + V(\mathbf{r}, t)
其中:
- m 是粒子的质量,
- \nabla^2 是拉普拉斯算符(描述空间中的二阶导数),
- V(\mathbf{r}, t) 是势能函数,依赖于位置和时间。
时间无关薛定谔方程
如果粒子的势能V(\mathbf{r})与时间无关,那么,哈密顿算符可以表示
\hat{H} = -\frac{\hbar^2}{2m} \nabla^2 + V(\mathbf{r}, t)
可以证明此时薛定谔方程有如下形式的解:
\psi(\mathbf{r}, t) = \phi(\mathbf{r})\chi(t)
只考虑\phi(\mathbf{r}),薛定谔方程可以简化为时间无关的形式:
\hat{H}\phi(\mathbf{r}) = E\phi(\mathbf{r})
其中:
- E 是系统的总能量(一个常数),
- \phi(\mathbf{r}) 是空间依赖的波函数,通常称为定态波函数。
注意,简单起见,后面统一使用符号 \psi(\mathbf{r}) 表示此处的 \phi(\mathbf{r})
球坐标系

图片来自wikipedia。
注意此处用的物理中的使用惯例(ISO 80000-2:2019),和数学中用的惯例的可能不一致。
- r 是径向坐标,表示原点到某一点的距离,
- \theta 是极角,表示从 z 轴向下的夹角(在 [0, \pi] 的范围内),
- \phi 是方位角,表示在 xy 平面内从 x 轴开始的夹角(在 [0, 2\pi] 的范围内)。
在球坐标系 (r, \theta, \phi) 下,拉普拉斯算符 \nabla^2 的形式比直角坐标系中的形式稍微复杂一些。它的具体表达式为:
\nabla^2 = \frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial}{\partial r} \right) + \frac{1}{r^2 \sin \theta} \frac{\partial}{\partial \theta} \left( \sin \theta \frac{\partial}{\partial \theta} \right) + \frac{1}{r^2 \sin^2 \theta} \frac{\partial^2}{\partial \phi^2}
此时,时间无关的薛定谔方程,变成了:
-\frac{\hbar^2}{2m} \left( \frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial}{\partial r} \right) + \frac{1}{r^2 \sin \theta} \frac{\partial}{\partial \theta} \left( \sin \theta \frac{\partial}{\partial \theta} \right) + \frac{1}{r^2 \sin^2 \theta} \frac{\partial^2}{\partial \phi^2} \right) \psi(r, \theta, \phi)
+ V(r) \psi(r, \theta, \phi) = E \psi(r, \theta, \phi)
径向方程与角度方程
使用分离变量法,假设波函数可以分离为径向部分和角度部分:
\psi(r, \theta, \phi) = R(r) Y(\theta, \phi)
其中:
- R(r) 是径向波函数,
- Y(\theta, \phi) 是角度部分波函数(球谐函数)。
代入薛定谔方程后,方程可以分离为两个独立的部分:一个是径向方程,另一个是角度方程。
径向方程:
\frac{d}{dr} \left( r^2 \frac{dR(r)}{dr} \right) + \left( \frac{2mr^2}{\hbar^2} \left( E - V(r) \right) - l(l+1) \right) R(r) = 0
这个方程描述了电子在径向方向上的行为,解这个方程可以得到电子在不同能级下的径向波函数。
角度方程:
\frac{1}{\sin \theta} \frac{\partial}{\partial \theta} \left( \sin \theta \frac{\partial Y(\theta, \phi)}{\partial \theta} \right) + \frac{1}{\sin^2 \theta} \frac{\partial^2 Y(\theta, \phi)}{\partial \phi^2} = -l(l+1) Y(\theta, \phi)
其解是球谐函数 Y_l^m(\theta, \phi),其中 l 是轨道角动量量子数,m 是磁量子数。
球谐函数是定义在球面上的特殊函数,广泛用于物理和数学领域,尤其是在球对称问题中,如量子力学中的原子轨道、经典力学中的引力场和电场,以及计算机图形学中的全局光照。
径向波函数
对于氢原子,前面的径向方程中
- E 是电子的能量,与量子数n有关。对氢原子来说,能级公式E_n=-\frac{13.6\text{eV}}{n^2}
- V(r) = -\frac{e^2}{4 \pi \epsilon_0 r} 是库仑势能,
通过一堆看不懂的数学技巧,最终可以解出来
R_{n,l}(r) = N_{n,l} \left( \frac{r}{a_0} \right)^l e^{-\frac{r}{n a_0}} L_{n-l-1}^{2l+1} \left( \frac{2r}{n a_0} \right)
其中:
- L_{n-l-1}^{2l+1} \left( \frac{2r}{n a_0} \right) 是拉盖尔多项式,
- n 是主量子数,表示电子的能级。
- a_0是波尔半径 \frac{4 \pi \epsilon_0 \hbar^2}{me^2}
- N_{n,l} 是归一化系数,公式附下面:
N_{n,l} = \left( \frac{2}{n a_0} \right)^{3/2} \sqrt{\frac{(n - l - 1)!}{2n (n + l)!}}
这样一来,就可以写python代码了(AI基本可以直接生成)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 | import numpy as np
from scipy.special import genlaguerre, factorial
from scipy.constants import physical_constants
import matplotlib.pyplot as plt
# Get the Bohr radius a_0
a_0 = physical_constants['Bohr radius'][0]
# Calculate the normalization constant N_{n,l}
def normalization_constant(n, l):
num = (2 / (n * a_0))**3 * factorial(n - l - 1)
denom = 2 * n * factorial(n + l)
return np.sqrt(num / denom)
# Define the radial wavefunction R_{n,l}(r)
def radial_wavefunction(n, l, r):
rho = 2 * r / (n * a_0) # Compute the dimensionless variable rho
laguerre_polynomial = genlaguerre(n - l - 1, 2 * l + 1) # Generalized Laguerre polynomial
normalization = normalization_constant(n, l) # Normalization constant
radial_part = rho**l * np.exp(-rho / 2) * laguerre_polynomial(rho) # Main part of the radial wavefunction
return normalization * radial_part
# Function to plot the radial wavefunction for given n and l
def plot_radial_wavefunction(n, l):
# Define the range of r values
r_values = np.linspace(0, 50 * a_0, 1000) # From 0 to 50 * a_0
# Compute the radial wavefunction
R_values = radial_wavefunction(n, l, r_values)
# Plot the result
plt.plot(r_values / a_0, R_values, label=f"R_{n},{l}(r)")
plt.xlabel(r"$r / a_0$")
plt.ylabel(r"$R_{n,l}(r)$")
plt.title(f"Radial Wavefunction for n={n}, l={l}")
plt.grid(True)
plt.legend()
plt.show()
# Example usage: Plot for n = 2, l = 0
plot_radial_wavefunction(2, 0)
|
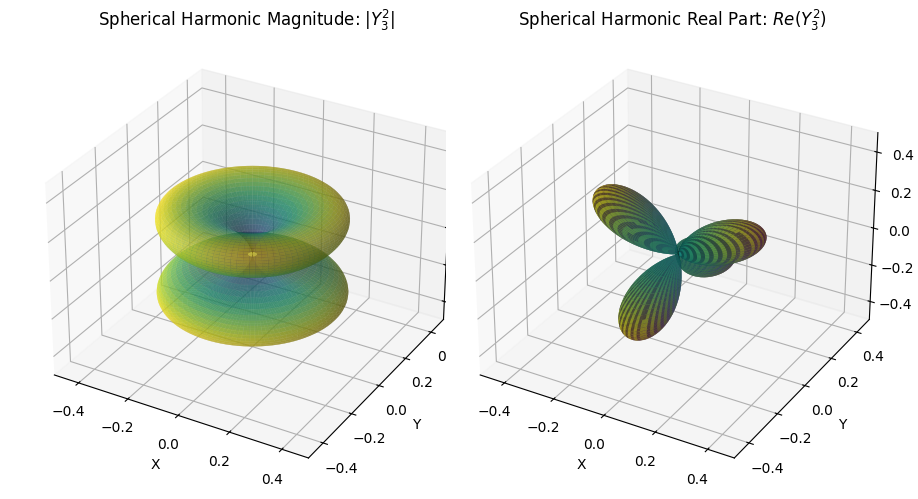
角向波函数(球谐函数)
球谐函数 Y_{l}^{m}(\theta, \phi) 是球坐标系下的两变量函数,定义在角度变量 \theta 和 \phi 上。其一般形式为:
Y_{l}^{m}(\theta, \phi) = \sqrt{\frac{(2l+1)}{4\pi} \frac{(l-m)!}{(l+m)!}} P_{l}^{m}(\cos\theta) e^{im\phi}
其中:
- l 是非负整数,称为角量子数或多极子阶数。
- m 是整数,满足 -l \leq m \leq l,称为磁量子数。
- \theta 是极角,取值范围 [0, \pi]。
- \phi 是方位角,取值范围 [0, 2\pi]。
- P_{l}^{m}(\cos\theta) 是连带勒让德多项式。
这个函数在python中有现成的,所以AI直接给出代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64 | import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.special import sph_harm
# Function to visualize both the magnitude and real part of the spherical harmonic
def plot_spherical_harmonic(l, m):
# Generate the range of angles
theta = np.linspace(0, np.pi, 100) # Polar angle θ from 0 to π
phi = np.linspace(0, 2 * np.pi, 100) # Azimuthal angle φ from 0 to 2π
theta, phi = np.meshgrid(theta, phi) # Create a meshgrid of angles
# Compute the spherical harmonic Y_l^m(θ, φ)
Y_lm = sph_harm(m, l, phi, theta)
# Calculate the magnitude |Y_l^m| (for one plot)
r_magnitude = np.abs(Y_lm)
# Calculate the real part Re(Y_l^m) (for the other plot)
r_real = np.real(Y_lm)
# Convert spherical coordinates to Cartesian coordinates for magnitude plot
x_mag = r_magnitude * np.sin(theta) * np.cos(phi)
y_mag = r_magnitude * np.sin(theta) * np.sin(phi)
z_mag = r_magnitude * np.cos(theta)
# Convert spherical coordinates to Cartesian coordinates for real part plot
x_real = r_real * np.sin(theta) * np.cos(phi)
y_real = r_real * np.sin(theta) * np.sin(phi)
z_real = r_real * np.cos(theta)
# Create a figure with two subplots
fig = plt.figure(figsize=(16, 6))
# Subplot 1: Magnitude |Y_l^m|
ax1 = fig.add_subplot(121, projection='3d')
ax1.plot_surface(x_mag, y_mag, z_mag, facecolors=plt.cm.viridis(r_magnitude / r_magnitude.max()),
rstride=1, cstride=1, alpha=0.6, edgecolor='none')
ax1.set_title(f"Spherical Harmonic Magnitude: $|Y_{l}^{m}|$")
ax1.set_xlim([-0.5, 0.5])
ax1.set_ylim([-0.5, 0.5])
ax1.set_zlim([-0.5, 0.5])
ax1.set_xlabel('X')
ax1.set_ylabel('Y')
ax1.set_zlabel('Z')
# Subplot 2: Real part Re(Y_l^m)
ax2 = fig.add_subplot(122, projection='3d')
ax2.plot_surface(x_real, y_real, z_real, facecolors=plt.cm.viridis((r_real - r_real.min()) / (r_real.max() - r_real.min())),
rstride=1, cstride=1, alpha=0.6, edgecolor='none')
ax2.set_title(f"Spherical Harmonic Real Part: $Re(Y_{l}^{m})$")
ax2.set_xlim([-0.5, 0.5])
ax2.set_ylim([-0.5, 0.5])
ax2.set_zlim([-0.5, 0.5])
ax2.set_xlabel('X')
ax2.set_ylabel('Y')
ax2.set_zlabel('Z')
# Show the figure
plt.tight_layout()
plt.show()
# Example: Plot both magnitude and real part for l = 3, m = 2
plot_spherical_harmonic(3, 2)
|

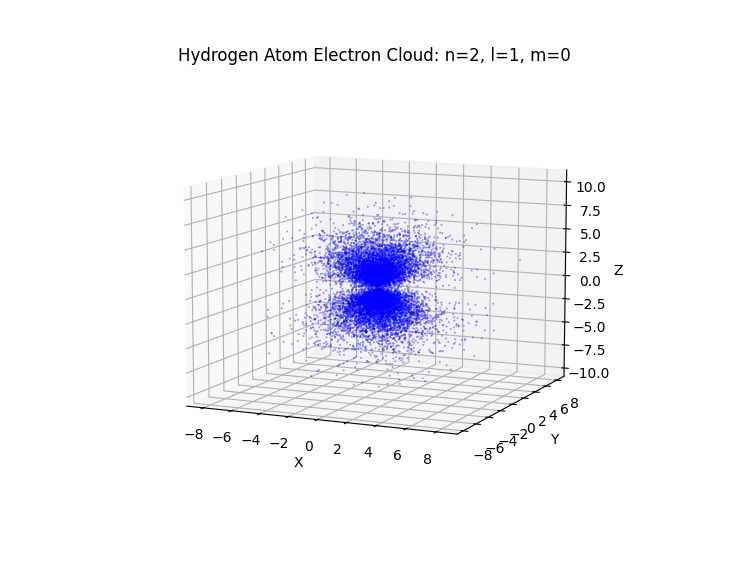
氢原子电子云
电子云图是电子在原子内的概率分布的可视化,它展示了电子在不同位置出现的概率。需要同时考虑径向和角向波函数。概率密度与波函数模平方成正比。
- 生成随机点(三维坐标下,用球坐标表示)
- 计算每个点的概率密度(计算波函数模值)
- 概率筛选(删除概率小的点)
- 转换为笛卡尔坐标
- 绘制点云
复数轨道
注意:此处绘制的是复数轨道的模平方,因为球谐函数通常是复数,具有实部和虚部。复数波函数带有相位信息,但其物理含义通常通过波函数模平方来体现。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72 | import numpy as np
import matplotlib.pyplot as plt
from scipy.special import sph_harm, genlaguerre, factorial
# Constants
a0 = 1.0 # Bohr radius (in atomic units)
# Radial wavefunction R_{n,l}(r) for hydrogen atom
def hydrogen_radial_wavefunction(n, l, r):
# Radial part of the wavefunction for hydrogen atom
rho = 2 * r / (n * a0)
# Normalization constant
norm = np.sqrt((2 / (n * a0))**3 * factorial(n - l - 1) / (2 * n * factorial(n + l)))
# Radial wavefunction
radial_part = norm * np.exp(-rho / 2) * rho**l * genlaguerre(n - l - 1, 2 * l + 1)(rho)
return radial_part
# Probability density function for hydrogen atom
def hydrogen_wavefunction_squared(n, l, m, r, theta, phi):
# Radial part
R_nl = hydrogen_radial_wavefunction(n, l, r)
# Angular part (spherical harmonics)
Y_lm = sph_harm(m, l, phi, theta)
# Return the square of the wavefunction (probability density)
return np.abs(R_nl * Y_lm)**2
# Generate random points in spherical coordinates
def random_points_in_sphere(num_points, n, l, m):
# Generate random spherical coordinates
r = np.random.rand(num_points) * 10 * a0 # Random radius within a reasonable range
theta = np.arccos(2 * np.random.rand(num_points) - 1) # Uniformly distributed cos(theta)
phi = np.random.rand(num_points) * 2 * np.pi # Uniformly distributed phi
# Compute the probability density at each point
prob_density = hydrogen_wavefunction_squared(n, l, m, r, theta, phi)
# Normalize the probabilities
prob_density /= prob_density.max()
# Filter points based on probability density (Monte Carlo sampling)
mask = np.random.rand(num_points) < prob_density
# Keep only the points that passed the filter
return r[mask], theta[mask], phi[mask]
# Convert spherical to Cartesian coordinates
def spherical_to_cartesian(r, theta, phi):
x = r * np.sin(theta) * np.cos(phi)
y = r * np.sin(theta) * np.sin(phi)
z = r * np.cos(theta)
return x, y, z
# Main function to plot the hydrogen atom electron cloud
def plot_hydrogen_cloud(n, l, m, num_points=100000):
# Generate random points in spherical coordinates
r, theta, phi = random_points_in_sphere(num_points, n, l, m)
# Convert spherical coordinates to Cartesian
x, y, z = spherical_to_cartesian(r, theta, phi)
# Plot the points
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, color='blue', s=0.1, alpha=0.6)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title(f'Hydrogen Atom Electron Cloud: n={n}, l={l}, m={m}')
plt.show()
# Example: Plot the electron cloud for the 2p orbital (n=2, l=1, m=0)
plot_hydrogen_cloud(n=2, l=1, m=0)
|
实数轨道
实轨道是通过将复数球谐函数的线性组合转换为实数形式来表示的。虽然球谐函数本质上是复数函数,但通过适当的线性组合,可以得到仅包含实数的轨道,这些轨道更符合直观的物理图像。
s-轨道:球对称的,只有 l=0 的情况,没有角动量方向,波函数是实数。
p-轨道:通过将复数球谐函数的线性组合转换为实数形式,我们可以得到三个常用的实轨道 p_x、p_y、p_z:
- p_x: 对应 Y_1^1 + Y_1^{-1} 的线性组合。(需要归一化?)
- p_y: 对应 Y_1^1 - Y_1^{-1} 的线性组合。
- p_z: 对应 Y_1^0。
这些轨道是直观的、方向明确的电子云形状,分别沿着 x、y、z 轴方向对称。
d-轨道:类似地,d-轨道可以通过 l=2 的复数球谐函数的线性组合得到五个实数轨道,如 d_{xy}、d_{xz}、d_{yz}、d_{z^2}、d_{x^2 - y^2}。
AI给出参考代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97 | import numpy as np
import matplotlib.pyplot as plt
from scipy.special import sph_harm, factorial
# Constants
a0 = 1.0 # Bohr radius (in atomic units)
# Radial wavefunction R_{n,l}(r) for hydrogen atom
def hydrogen_radial_wavefunction(n, l, r):
rho = 2 * r / (n * a0)
norm = np.sqrt((2 / (n * a0))**3 * factorial(n - l - 1) / (2 * n * factorial(n + l)))
radial_part = norm * np.exp(-rho / 2) * rho**l
return radial_part
# Probability density function for hydrogen atom
def hydrogen_wavefunction_squared(n, l, m, r, theta, phi):
R_nl = hydrogen_radial_wavefunction(n, l, r)
Y_lm = sph_harm(m, l, phi, theta)
return np.abs(R_nl * Y_lm)**2
# Generate random points in spherical coordinates
def random_points_in_sphere(num_points, n, l, m):
r = np.random.rand(num_points) * 10 * a0 # Random radius within a reasonable range
theta = np.arccos(2 * np.random.rand(num_points) - 1) # Uniformly distributed cos(theta)
phi = np.random.rand(num_points) * 2 * np.pi # Uniformly distributed phi
prob_density = hydrogen_wavefunction_squared(n, l, m, r, theta, phi)
# Check if max(prob_density) is non-zero before normalizing
max_density = prob_density.max()
if max_density > 0: # Avoid division by zero
prob_density /= max_density
# Loosen filtering condition
mask = np.random.rand(num_points) < prob_density * 5 # Loosen the filtering condition
print(f"Number of points before filtering: {num_points}, after filtering: {np.sum(mask)}")
return r[mask], theta[mask], phi[mask]
# Convert spherical to Cartesian coordinates
def spherical_to_cartesian(r, theta, phi):
x = r * np.sin(theta) * np.cos(phi)
y = r * np.sin(theta) * np.sin(phi)
z = r * np.cos(theta)
return x, y, z
# Real spherical harmonics (p_x, p_y, p_z orbitals)
def real_spherical_harmonics(l, m, theta, phi):
if l == 1:
if m == 'p_x':
# p_x: Re(Y_1^1 + Y_1^-1)
return (sph_harm(1, 1, phi, theta).real + sph_harm(-1, 1, phi, theta).real)
elif m == 'p_y':
# p_y: Im(Y_1^1 - Y_1^-1)
return (sph_harm(1, 1, phi, theta).imag - sph_harm(-1, 1, phi, theta).imag)
elif m == 'p_z':
# p_z: Re(Y_1^0)
return sph_harm(0, 1, phi, theta).real
elif l == 2:
if m == 'd_xy':
return sph_harm(2, 2, phi, theta).imag
elif m == 'd_xz':
return sph_harm(1, 2, phi, theta).real
elif m == 'd_yz':
return sph_harm(1, 2, phi, theta).imag
elif m == 'd_z2':
return sph_harm(0, 2, phi, theta).real
elif m == 'd_x2_y2':
return sph_harm(2, 2, phi, theta).real
else:
raise ValueError("Unsupported orbital")
# Main function to plot the hydrogen atom real orbitals
def plot_real_hydrogen_orbital(n, l, m, num_points=100000):
r, theta, phi = random_points_in_sphere(num_points, n, l, 0) # m=0, radial sampling
# Real spherical harmonics
Y_lm_real = real_spherical_harmonics(l, m, theta, phi)
prob_density = np.abs(hydrogen_radial_wavefunction(n, l, r) * Y_lm_real)**2
# Check if max(prob_density) is non-zero before normalizing
max_density = prob_density.max()
if max_density > 0: # Avoid division by zero
prob_density /= max_density
# Convert spherical to Cartesian coordinates
x, y, z = spherical_to_cartesian(r, theta, phi)
# Plot the points
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, color='blue', s=0.1, alpha=0.6)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title(f'Hydrogen Atom Real Orbital: n={n}, l={l}, m={m}')
plt.show()
# Example: Plot the real orbital for the p_x orbital (n=2, l=1, m='p_x')
plot_real_hydrogen_orbital(n=2, l=1, m='p_x')
|
参考
- https://liam-ilan.github.io/electron-orbitals/
- https://en.wikipedia.org/wiki/Wave_function#Hydrogen_atom
- https://ssebastianmag.medium.com/computational-physics-with-python-hydrogen-wavefunctions-electron-density-plots-8fede44b7b12
- https://www.researchgate.net/publication/375039550_Quantum_Mechanical_Hydrogen_Atom_Model_Visualised_using_Python
- https://physics.stackexchange.com/questions/190726/what-is-the-difference-between-real-orbital-complex-orbital/190730#190730
- https://github.com/PyCOMPLETE/PyECLOUD
- https://github.com/Niuskir/Electron-Orbitals-Blender-3D
- https://github.com/damontallen/Orbitals/blob/master/Hydrogen%20Orbitals%20(Feb%2018,%202014)%20(dynamic%20entry).ipynb
- https://in2infinity.com/2d-orbital-geometry-of-the-electron-cloud/



