RSA加密算法是一种非对称加密算法（public-key cryptosystem）。它是由 罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和 伦纳德·阿德曼（Leonard Adleman）在1977年一起提出的。当时他们三人都在MIT工作。RSA 是他们三人姓氏开头字母拼成的。RSA算法包括四个步骤：密钥生成、密钥分发、加密和解密。

非对称公钥-私钥密码系统的想法由 Whitfield Diffie 和 Martin Hellman 提出，他们于 1976 年发表了这个概念。在这之前，所有的加密方法都是同一种模式——对称加密算法（Symmetric-key algorithm）。

RSA 原理

RSA 背后的基本原理是观察到找到三个非常大的正整数 e、d 和 n 是可行的，这样对所有整数 m（0 ≤ m < n）进行模幂运算：

1

(m**e)**d ≡ m (mod n)

其中，≡ 表示模同余（modular congruence)。同除以n时，(m**e)**d与m有相同的余数。

• 公钥由整数 n 和 e 表示
• 私钥由整数 d 表示（解密过程中也会使用 n，也可视为私钥的一部分）
• m 代表消息

RSA的安全性在于：已知公钥n和e，难以推导出私钥d。

注意：尽管通常将公钥e用于加密，私钥d用于解密。数学上，d和e的顺序完全是可以交换的：

1

(m**d)**e ≡ m (mod n)

Key生成

生成n、d、和 e

1. 选择两个大质数 p 和 q

• 为了使分解更加困难，p和q应该随机选择，都很大并且有很大的差异。选择它们的标准方法是：选择随机整数并使用质性测试，直到找到两个质数。
• p 和 q 应该保密。

2. 计算 n = pq

• n 用作公钥和私钥的模数。 它的长度通常以位表示，即密钥长度。常说的RSA 1024、2048、4096就是这个值的二进制位数。

• n 作为公钥的一部分发布。

3. 计算 λ(n)

早期的RSA的文章中，用的φ(p)，而不是 λ(n)。

λ 是Carmichael's totient function 函数。它和 Euler totient function 有如下关系：

如果两个正整数，除了1之外，没有其他公因子，这两个数就是互质关系（coprime)。不是质数的两个数可以是互质关系，比如21和8。欧拉函数φ(n)用于表示，对于正整数n，在小于等于n的正整数中，有多少个与n构成互质关系。

因为 n = pq，所以 λ(n) = lcm(λ(p), λ(q))

因为 p 和 q 是质数，所以λ(p) = φ(p) = p − 1，λ(q ) = q − 1

• λ(n) = lcm(p − 1, q − 1)。lcm可以通过欧几里德算法计算，因为lcm(a,b)=|ab|/gcd(a,b)

• λ(n) 是保密的。

lcm：Least common multiple（最小公倍数）

gcd：Greatest common divisor（最大公约数）

4. 选择一个整数 e

早期的RSA文章，都是选择d，而后计算e。但现在主流的实现，都是选择e，而后计算d。

e的选择需要满足： 2 < e < λ(n) 且 gcd(e, λ(n)) = 1； 也就是说，e 和 λ(n) 互质。

• e 具有较短的位长度和较小的汉明权重，可以实现更高效的加密 – 最常用的 e 值为 216 + 1 = 65537。e 的最小（也是最快）可能值为 3，但如此小的值 e 已被证明在某些设置中不太安全。
• e 作为公钥的一部分发布。

5. 确定 d

1

 d ≡  e^(-1) (mod λ(n))

d 是 e 模 λ(n) 的模乘逆。求解 d 方程 de ≡ 1 (mod λ(n))。

• d 作为私钥指数保密。

公钥由模数 n 和公共（或加密）指数 e 组成。 私钥由私有（或解密）指数 d 组成，必须保密。 p、q 和 λ(n) 也必须保密，因为它们可用于计算 d。 事实上，在计算 d 后它们都可以被丢弃。

n已知，如果能够分解n，那么p和q就能被计算出来，进而找到d。破解RSA的难点在于n的因数分解，对于大整数的因数分解，目前没有高效的算法。

例子

生成Key，全程涉及6个数字：p、q、n、lam(n)、e、d。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

import math

# 1 选择两个素数p,q
p = 61
q = 53

# 2 计算n=p*q, 结果 3233
n = p * q

# 3 计算lam(n)=lcm((p-1), (q-1)), 结果 780
lam_n = math.lcm((p - 1), (q - 1))

# 4 选择一个整数e, 1<e<lam(n), 且e与lam(n)互质
e = 17

# 5 计算d, 使得e*d=1(mod lam(n)), 结果 413
#   考虑 e*d = 1+k*lam(n), k 为任意正整数

for k in range(1, 1000):
    if (1 + k * lam_n) % e == 0:
        d = (1 + k * lam_n) // e
        break

# 6 公钥为(n,e), 私钥为(n,d)
print(f"公钥为(n,e): ({n},{e})")
print(f"私钥为(n,d): ({n},{d})")

结果：

1
2

公钥为(n,e): (3233,17)
私钥为(n,d): (3233,413)

使用上面的公钥和私钥，加密解密

1
2
3
4
5

m = 65
# 加密，结果 2790
c = m ** 17 % 3233
# 解密
m2 = c ** 413 % 3233

OpenSSL 查看key内容

可以使用openssl命令查看一个rsa公钥文件的内容

1

openssl rsa -pubin -in rsa_2048.pub -text

输出如下（包含Modulus：n 和 Exponent：e）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

Public-Key: (2048 bit)
Modulus:
    00:d9:69:38:fd:16:53:95:5d:96:a7:6f:26:32:5c:
    ......
    05:24:e5:68:53:3b:14:c9:95:3f:72:dd:5f:35:4f:
    29:6f
Exponent: 65537 (0x10001)
writing RSA key
-----BEGIN PUBLIC KEY-----
MIIBIjANBgkqhkiG9w0BAQEFAAOCAQ8AMIIBCgKCAQEA2Wk4/RZTlV2Wp28mMlzG
......
bwIDAQAB
-----END PUBLIC KEY-----

也可以使用openssl命令查看一个rsa私钥文件的内容

1

openssl rsa -in rsa_2048.key -text

私钥中，除了前面提到的：

• prime1：p
• prime2：q
• modulus：N = p * q
• publicExponent：e
• privateExponent：d

还有另外三个值（这三个值有助于更高效地执行解密操作）：

• exponent1：d (mod p-1)
• exponent2：d (mod q-1)
• coefficient：q^(-1) (mod p)

具体输出如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

Private-Key: (2048 bit, 2 primes)
modulus:
    00:d9:69:38:fd:16:53:95:5d:96:a7:6f:26:32:5c:
    ......
    05:24:e5:68:53:3b:14:c9:95:3f:72:dd:5f:35:4f:
    29:6f
publicExponent: 65537 (0x10001)
privateExponent:
    47:09:63:f7:01:e4:06:92:61:46:cd:00:f0:84:b2:
    ......
    f8:a9:9a:56:34:a5:1a:ec:33:1e:a4:47:d9:3a:da:
    bd
prime1:
    00:f0:71:f0:d6:75:d6:1b:33:81:9a:30:c7:ee:95:
    .......
    49:c8:43:94:b9:b9:dc:74:d5
prime2:
    00:e7:79:cf:6b:1d:08:35:15:ca:f3:d8:1b:f0:02:
    ......
    56:fd:60:57:b5:bd:b1:d7:33
exponent1:
    00:8c:47:3d:66:31:6b:4f:85:56:38:79:fb:3a:f3:
    ......
    66:04:63:81:32:75:ff:eb:5d
exponent2:
    00:c9:6b:2a:3c:b7:87:83:c1:d1:d7:3b:4e:9c:1b:
    ......
    7c:92:7f:f9:f2:6f:fd:47:17
coefficient:
    00:86:81:97:52:aa:2e:ac:68:23:6f:d7:e1:2c:04:
    ......
    51:de:13:be:70:dd:4c:40:29
writing RSA key
-----BEGIN PRIVATE KEY-----
MIIEvwIBADANBgkqhkiG9w0BAQEFAASCBKkwggSlAgEAAoIBAQDZaTj9FlOVXZan
......
pX6lk6dw5kSVHFHeE75w3UxAKQ==
-----END PRIVATE KEY-----

RFC3447

公钥：

1
2
3
4
5
6
7
8
9

A.1.1 RSA public key syntax

   An RSA public key should be represented with the ASN.1 type
   RSAPublicKey:

      RSAPublicKey ::= SEQUENCE {
          modulus           INTEGER,  -- n
          publicExponent    INTEGER   -- e
      }

私钥：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

A.1.2 RSA private key syntax

   An RSA private key should be represented with the ASN.1 type
   RSAPrivateKey:

      RSAPrivateKey ::= SEQUENCE {
          version           Version,
          modulus           INTEGER,  -- n
          publicExponent    INTEGER,  -- e
          privateExponent   INTEGER,  -- d
          prime1            INTEGER,  -- p
          prime2            INTEGER,  -- q
          exponent1         INTEGER,  -- d mod (p-1)
          exponent2         INTEGER,  -- d mod (q-1)
          coefficient       INTEGER,  -- (inverse of q) mod p
          otherPrimeInfos   OtherPrimeInfos OPTIONAL
      }

填充

RSA的短明文可导致密文容易被攻击。给明文填充伪数据可以给攻击制造困难。

OpenSSL给出如下选项。

• RSA_PKCS1_PADDING，填充至少11字节
• RSA_NO_PADDING ，明文前面填充0，如果明文开头有0，解密后会被当做填充去掉
• RSA_PKCS1_OAEP_PADDING ，填充至少41字节，(只用于加密和解密)。
• RSA_X931_PADDING（只用于 签名）
• RSA_PKCS1_PSS_PADDING（只用于 签名和验签）
• RSA_PKCS1_WITH_TLS_PADDING（只用于解密，TLS RSA的ClientKeyExchange消息）

微软.Net中给出：

• RSAEncryptionPaddingMode
  • Oaep：推荐用于新程序
  • Pkcs1：PKCS#1 v1.5. 兼容现有程序
• RSASignaturePaddingMode
  • Pkcs1：PKCS#1 v1.5 兼容现有程序
  • Pss： 推荐用于新程序

PKCS1（PKCS#1 v1.5)

PKCS#1 标准的早期版本（最高版本 1.5）， 主要用于跟老应用的兼容。

消息M的长度(mLen)至少比RSA模数n的长度(k)要短11。因为要保证随机非零填充内容PS的长度至少为8。

对于加密操作，填充格式如下：

1

EM = 0x00 || 0x02 || PS || 0x00 || M

对于签名操作，填充如下：

1

EM = 0x00 || 0x01 || PS || 0x00 || T

在 Crypto 1998 上，Bleichenbacher 表明该版本容易受到实际的自适应选择密文攻击。

任何新应用程序都应使用 OAEP，并且应尽可能替换 PKCS#1 v1.5 填充。对签名处理要考虑概率签名方案 (RSA-PSS)。

OAEP

OAEP：Optimal Asymmetric Encryption Padding

OAEP填充模式对于原文长度要求：原文长度 <= 密钥模长 - (2 * 原文的摘要值长度) - 2

常见摘要值的长度（当用SHA-1时，原文比模长要短至少41字节）：

• SHA-1: 20字节
• SHA-256: 32字节
• SHA-384: 48字节
• SHA-512: 64字节

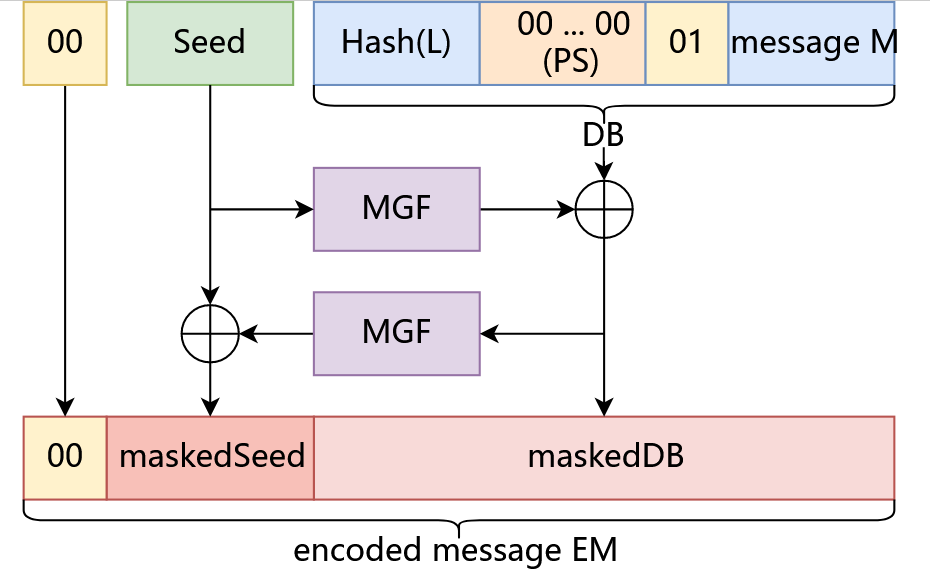
MGF

MGF：Mask Generation function

• 类似于哈希函数，但不同于哈希函数的输出大小固定，MGF的输出长度是可变的。
• 接受任意长度的输入，可给出任意长度的输出
• 同样的输入，输出结果是确定的

PSS

PSS：Probabilistic Signature Scheme

与传统PKCS#1 v1.5方式相比，PSS签名算法引入了随机性。

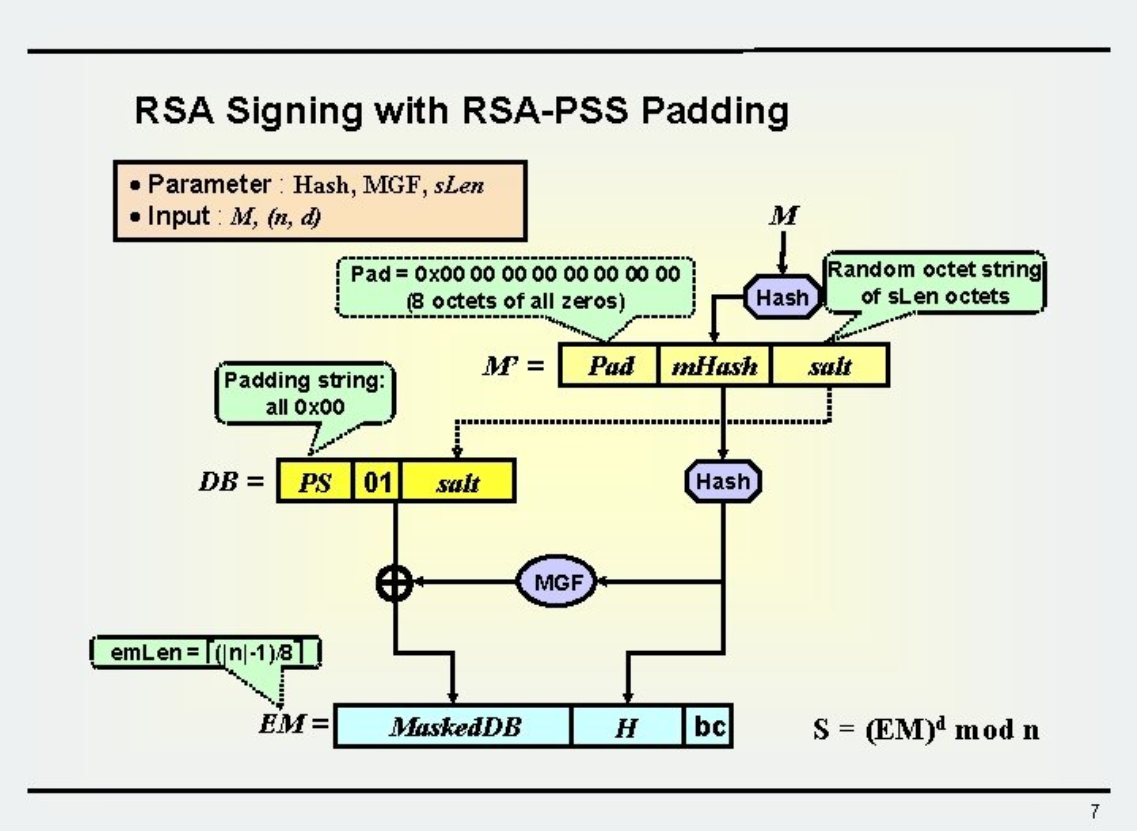
图片来源：https://slidetodoc.com/lect-15-digital-signatures-rsa-el-gamal-dsa/

这个东西太复杂了，简单看看它的反操作——签名验证流程：

• 解密：拿到签名S后，使用公钥进行RSA解密操作，得到解密后的EM。最后一个字节如不是0xbc，签名无效。
• 分隔 EM：分隔出哈希值H和MaskedDB。（哈希值H长度 由哈希算法确定）
• 计算 Salt：计算出DB值，分隔出PS和salt值，如果PS不是全0，签名无效。（salt长度一般与哈希值H长度一致）
• 构建M’：计算哈希值mHash，添加salt，建构出M‘
• 校验：计算M‘的哈希值，与H进行比较。如不相等，签名无效。

参考

• https://en.wikipedia.org/wiki/RSA_(cryptosystem)
• https://en.wikipedia.org/wiki/Optimal_asymmetric_encryption_padding
• https://www.di-mgt.com.au/crt_rsa.html
• https://www.rfc-editor.org/rfc/rfc3447
• https://www.51cto.com/article/663141.html